Question Number 37601 by prof Abdo imad last updated on 15/Jun/18
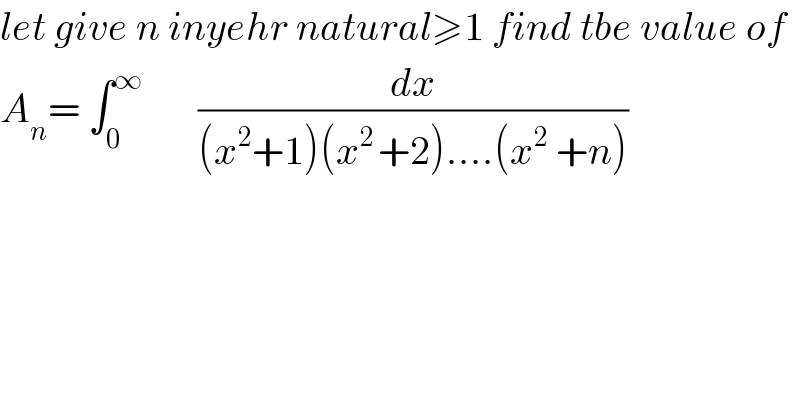
$${let}\:{give}\:{n}\:{inyehr}\:{natural}\geqslant\mathrm{1}\:{find}\:{tbe}\:{value}\:{of} \\ $$$${A}_{{n}} =\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}\:} +\mathrm{2}\right)….\left({x}^{\mathrm{2}} \:+{n}\right)} \\ $$
Commented by math khazana by abdo last updated on 17/Jun/18
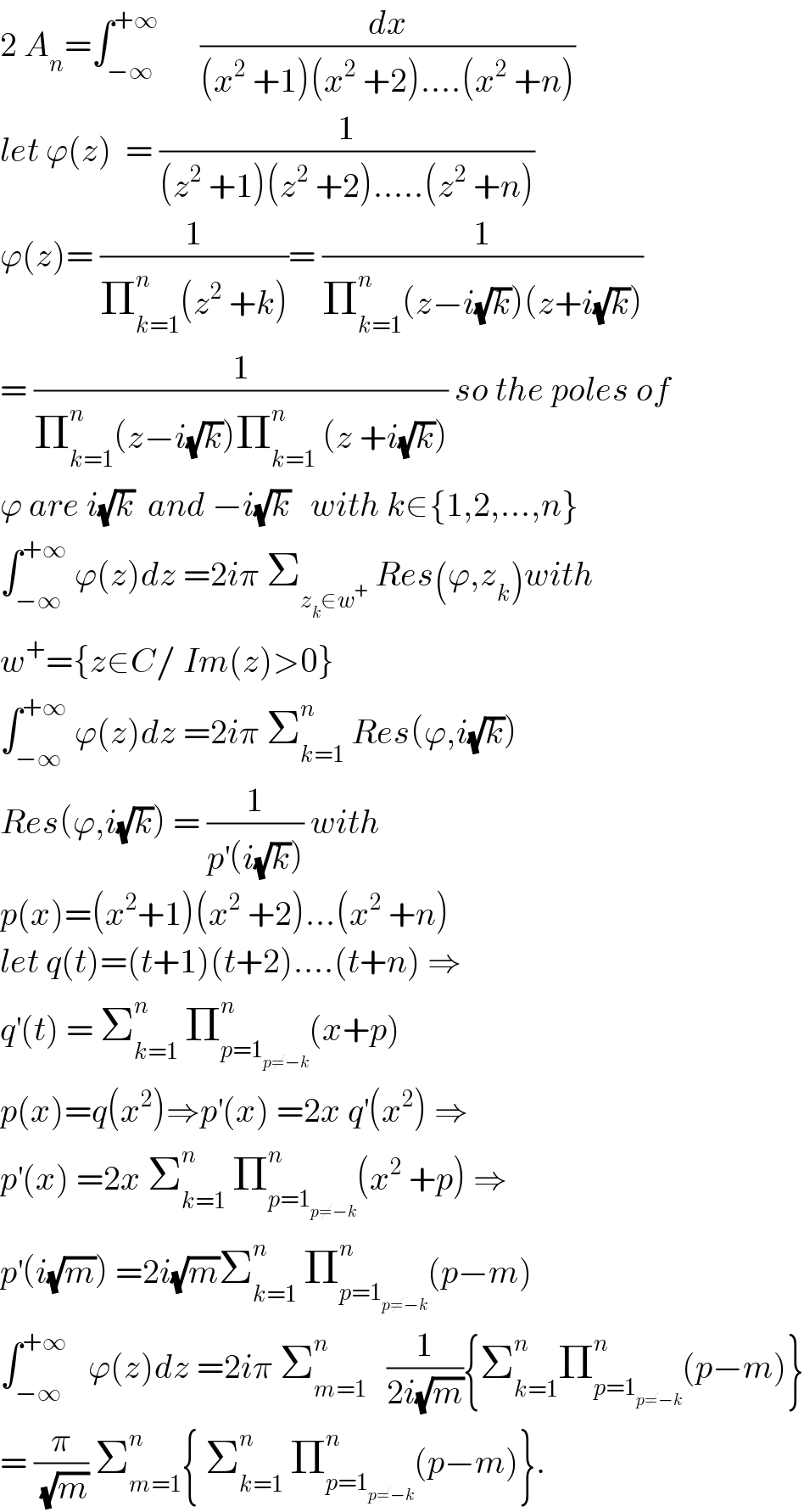
$$\mathrm{2}\:{A}_{{n}} =\int_{−\infty} ^{+\infty} \:\:\:\:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{2}\right)….\left({x}^{\mathrm{2}} \:+{n}\right)} \\ $$$${let}\:\varphi\left({z}\right)\:\:=\:\frac{\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)\left({z}^{\mathrm{2}} \:+\mathrm{2}\right)…..\left({z}^{\mathrm{2}} \:+{n}\right)} \\ $$$$\varphi\left({z}\right)=\:\frac{\mathrm{1}}{\prod_{{k}=\mathrm{1}} ^{{n}} \left({z}^{\mathrm{2}} \:+{k}\right)}=\:\frac{\mathrm{1}}{\prod_{{k}=\mathrm{1}} ^{{n}} \left({z}−{i}\sqrt{{k}}\right)\left({z}+{i}\sqrt{{k}}\right)} \\ $$$$=\:\frac{\mathrm{1}}{\prod_{{k}=\mathrm{1}} ^{{n}} \left({z}−{i}\sqrt{{k}}\right)\prod_{{k}=\mathrm{1}} ^{{n}} \:\left({z}\:+{i}\sqrt{{k}}\right)}\:{so}\:{the}\:{poles}\:{of} \\ $$$$\varphi\:{are}\:{i}\sqrt{{k}}\:\:{and}\:−{i}\sqrt{{k}}\:\:\:{with}\:{k}\in\left\{\mathrm{1},\mathrm{2},…,{n}\right\} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\sum_{{z}_{{k}} \in{w}^{+} } \:{Res}\left(\varphi,{z}_{{k}} \right){with} \\ $$$${w}^{+} =\left\{{z}\in{C}/\:{Im}\left({z}\right)>\mathrm{0}\right\} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{Res}\left(\varphi,{i}\sqrt{{k}}\right) \\ $$$${Res}\left(\varphi,{i}\sqrt{{k}}\right)\:=\:\frac{\mathrm{1}}{{p}^{'} \left({i}\sqrt{{k}}\right)}\:{with}\: \\ $$$${p}\left({x}\right)=\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{2}} \:+\mathrm{2}\right)…\left({x}^{\mathrm{2}} \:+{n}\right) \\ $$$${let}\:{q}\left({t}\right)=\left({t}+\mathrm{1}\right)\left({t}+\mathrm{2}\right)….\left({t}+{n}\right)\:\Rightarrow \\ $$$${q}^{'} \left({t}\right)\:=\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\prod_{{p}=\mathrm{1}_{{p}\neq−{k}} } ^{{n}} \left({x}+{p}\right) \\ $$$${p}\left({x}\right)={q}\left({x}^{\mathrm{2}} \right)\Rightarrow{p}^{'} \left({x}\right)\:=\mathrm{2}{x}\:{q}^{'} \left({x}^{\mathrm{2}} \right)\:\Rightarrow \\ $$$${p}^{'} \left({x}\right)\:=\mathrm{2}{x}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\prod_{{p}=\mathrm{1}_{{p}\neq−{k}} } ^{{n}} \left({x}^{\mathrm{2}} \:+{p}\right)\:\Rightarrow \\ $$$${p}^{'} \left({i}\sqrt{{m}}\right)\:=\mathrm{2}{i}\sqrt{{m}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\prod_{{p}=\mathrm{1}_{{p}\neq−{k}} } ^{{n}} \left({p}−{m}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:\:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\sum_{{m}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{{m}}}\left\{\sum_{{k}=\mathrm{1}} ^{{n}} \prod_{{p}=\mathrm{1}_{{p}\neq−{k}} } ^{{n}} \left({p}−{m}\right)\right\} \\ $$$$=\:\frac{\pi}{\:\sqrt{{m}}}\:\sum_{{m}=\mathrm{1}} ^{{n}} \left\{\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\prod_{{p}=\mathrm{1}_{{p}\neq−{k}} } ^{{n}} \left({p}−{m}\right)\right\}. \\ $$
Commented by math khazana by abdo last updated on 17/Jun/18
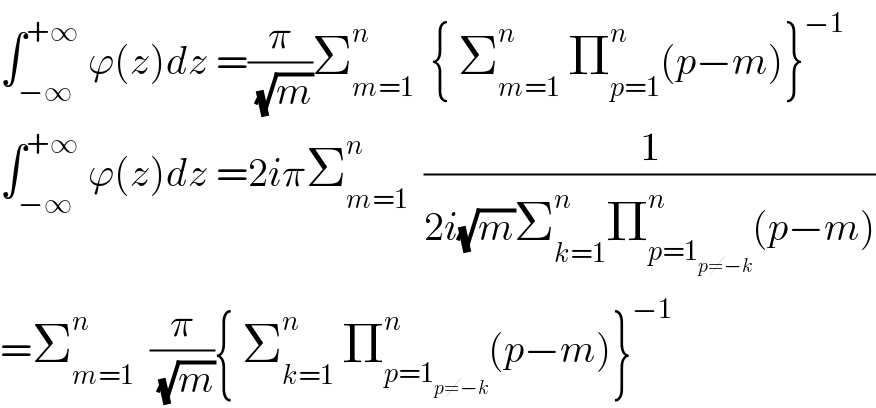
$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\pi}{\:\sqrt{{m}}}\sum_{{m}=\mathrm{1}} ^{{n}} \:\:\left\{\:\sum_{{m}=\mathrm{1}} ^{{n}} \:\prod_{{p}=\mathrm{1}} ^{{n}} \left({p}−{m}\right)\right\}^{−\mathrm{1}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\sum_{{m}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{{m}}\sum_{{k}=\mathrm{1}} ^{{n}} \prod_{{p}=\mathrm{1}_{{p}\neq−{k}} } ^{{n}} \left({p}−{m}\right)} \\ $$$$=\sum_{{m}=\mathrm{1}} ^{{n}} \:\:\frac{\pi}{\:\sqrt{{m}}}\left\{\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\prod_{{p}=\mathrm{1}_{{p}\neq−{k}} } ^{{n}} \left({p}−{m}\right)\right\}^{−\mathrm{1}} \\ $$
