Question Number 103154 by Dwaipayan Shikari last updated on 13/Jul/20
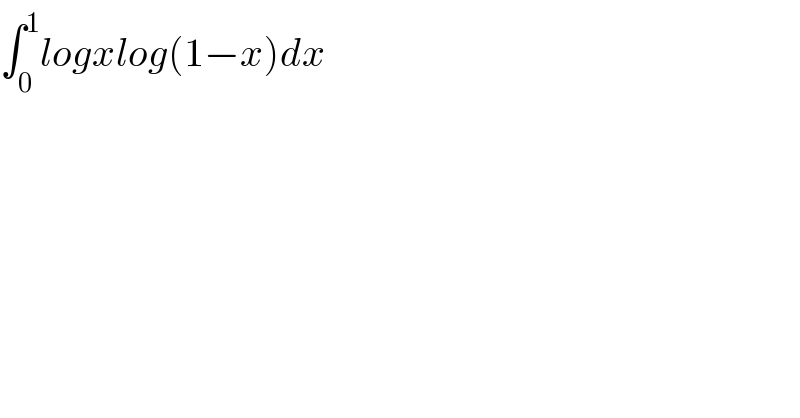
$$\int_{\mathrm{0}} ^{\mathrm{1}} {logxlog}\left(\mathrm{1}−{x}\right){dx} \\ $$
Answered by OlafThorendsen last updated on 13/Jul/20
![I = ∫_0 ^1 lnxln(1−x)dx −(1/(1−x)) = −Σ_(n=0) ^∞ x^n ln(1−x) = −Σ_(n=0) ^∞ (x^(n+1) /(n+1)) = −Σ_(n=1) ^∞ (x^n /n) I = −∫_0 ^1 lnxΣ_(n=1) ^∞ (x^n /n)dx I = −Σ_(n=1) ^∞ (1/n)∫_0 ^1 x^n lnxdx I_n = −∫_0 ^1 x^n lnxdx I_n = −[(x^(n+1) /(n+1))lnx]_0 ^1 +∫_0 ^1 (x^(n+1) /(n+1)).(1/x)dx I_n = 0+∫_0 ^1 (x^n /(n+1))dx = [(x^(n+1) /((n+1)^2 ))]_0 ^1 I_n = (1/((n+1)^2 )) I = Σ_(n=1) ^∞ (1/n)I_n = Σ_(n=1) ^∞ (1/(n(n+1)^2 )) I = Σ_(n=1) ^∞ ((1/n)−(1/(n+1))−(1/((n+1)^2 ))) Σ_(n=1) ^∞ ((1/n)−(1/(n+1))) = (1−(1/2))+((1/2)−(1/3))+... Σ_(n=1) ^∞ ((1/n)−(1/(n+1))) = 1 I = 1−Σ_(n=1) ^∞ (1/((n+1)^2 )) I = 1−Σ_(n=2) ^∞ (1/n^2 ) I = 2−Σ_(n=1) ^∞ (1/n^2 ) I = 2−ζ(2) = 2−(π^2 /6)](https://www.tinkutara.com/question/Q103174.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}{x}\mathrm{ln}\left(\mathrm{1}−{x}\right){dx} \\ $$$$−\frac{\mathrm{1}}{\mathrm{1}−{x}}\:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \\ $$$$\mathrm{ln}\left(\mathrm{1}−{x}\right)\:=\:−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}} \\ $$$$\mathrm{I}\:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}{x}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}{dx} \\ $$$$\mathrm{I}\:=\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \mathrm{ln}{xdx} \\ $$$$\mathrm{I}_{{n}} \:=\:−\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{n}} \mathrm{ln}{xdx} \\ $$$$\mathrm{I}_{{n}} \:=\:−\left[\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\mathrm{ln}{x}\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}.\frac{\mathrm{1}}{{x}}{dx} \\ $$$$\mathrm{I}_{{n}} \:=\:\mathrm{0}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} }{{n}+\mathrm{1}}{dx}\:=\:\left[\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{I}_{{n}} \:=\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\mathrm{I}_{{n}} \:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)\:=\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right)+… \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)\:=\:\mathrm{1} \\ $$$$\mathrm{I}\:=\:\mathrm{1}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\mathrm{1}−\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\mathrm{2}−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$\mathrm{I}\:=\:\mathrm{2}−\zeta\left(\mathrm{2}\right)\:=\:\mathrm{2}−\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$
Commented by Dwaipayan Shikari last updated on 13/Jul/20

$${Great}\:{sir}! \\ $$
Answered by bobhans last updated on 13/Jul/20
![I = ∫_0 ^1 ln(x) ln(1−x) dx by Maclaurin series ln(1−x) = −Σ_(n=1) ^∞ (x^n /n) we obtain I=−∫_0 ^1 ln(x)Σ_(n=1) ^∞ (x^n /n) dx I = −Σ_(n=1) ^∞ (1/n)∫_0 ^1 x^n ln(x) dx [ by parts ] { ((u = ln(x))),((dv = x^n dx )) :} I=−Σ_(n=1) ^∞ (1/n)∣((x^(n+1) /(n+1)) ln(x)−(x^(n+1) /((n+1)^2 )))∣_0 ^1 I= Σ_(n=1) ^∞ (1/(n(n+1)^2 )) [ by L′Hopital rule′s] I= Σ_(n=1) ^∞ ((1/n)−(1/(n+1))−(1/((n+1)^2 ))) the first series Σ_(n=1) ^∞ ((1/n)−(1/(n+1))) is telescoping ⇒ lim_(p→∞) Σ_(n=1) ^p ((1/n)−(1/(n+1))) = lim_(p→∞) (1−(1/(p+1))) = 1 now the second series Σ_(n=1) ^∞ (1/((n+1)^2 )) = Σ_(k=2) ^∞ (1/k^2 ) = −1+Σ_(k=1) ^∞ (1/k^2 ) = −1+(π^2 /6) . therefore I = ∫_0 ^1 ln(x) ln(1−x)dx = 1−(−1+(π^2 /6)) = 2−(π^2 /6) . ★](https://www.tinkutara.com/question/Q103210.png)
$${I}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{ln}\left({x}\right)\:\mathrm{ln}\left(\mathrm{1}−{x}\right)\:{dx}\: \\ $$$${by}\:{Maclaurin}\:{series}\: \\ $$$$\mathrm{ln}\left(\mathrm{1}−{x}\right)\:=\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}\: \\ $$$${we}\:{obtain}\:{I}=−\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{ln}\left({x}\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}\:{dx}\: \\ $$$${I}\:=\:−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:{x}^{{n}} \:\mathrm{ln}\left({x}\right)\:{dx}\:\left[\:{by}\:{parts}\:\right] \\ $$$$\begin{cases}{{u}\:=\:\mathrm{ln}\left({x}\right)}\\{{dv}\:=\:{x}^{{n}} \:{dx}\:}\end{cases} \\ $$$${I}=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\mid\left(\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:\mathrm{ln}\left({x}\right)−\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$${I}=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:\left[\:{by}\:{L}'{Hopital}\:{rule}'{s}\right] \\ $$$${I}=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$${the}\:{first}\:{series}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)\:{is} \\ $$$${telescoping}\:\Rightarrow\:\underset{{p}\rightarrow\infty} {\mathrm{lim}}\:\underset{{n}=\mathrm{1}} {\overset{{p}} {\sum}}\:\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\:\underset{{p}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}−\frac{\mathrm{1}}{{p}+\mathrm{1}}\right)\:=\:\mathrm{1}\: \\ $$$${now}\:{the}\:{second}\:{series}\: \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\:=\:−\mathrm{1}+\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} } \\ $$$$=\:−\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:. \\ $$$${therefore}\:{I}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{ln}\left({x}\right)\:\mathrm{ln}\left(\mathrm{1}−{x}\right){dx}\:=\: \\ $$$$\mathrm{1}−\left(−\mathrm{1}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\right)\:=\:\mathrm{2}−\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:.\:\bigstar\: \\ $$
