Question Number 37633 by math khazana by abdo last updated on 16/Jun/18
![find ∫_0 ^(+∞) [ x e^(−x) ]dx](https://www.tinkutara.com/question/Q37633.png)
$${find}\:\:\int_{\mathrm{0}} ^{+\infty} \left[\:\:{x}\:{e}^{−{x}} \right]{dx} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Jun/18
![if [xe^(−x) ] denote greatest integer function then value of [xe^(−x) ]=0 so given intregal value is zero](https://www.tinkutara.com/question/Q37653.png)
$$\: \\ $$$${if}\:\left[{xe}^{−{x}} \right]\:{denote}\:{greatest}\:{integer}\:{function} \\ $$$${then}\:\:{value}\:{of}\:\left[{xe}^{−{x}} \right]=\mathrm{0} \\ $$$${so}\:{given}\:{intregal}\:{value}\:{is}\:{zero} \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 16/Jun/18
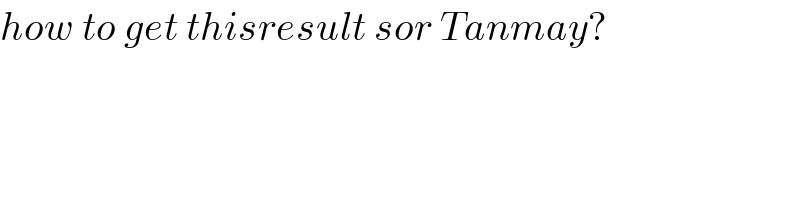
$${how}\:{to}\:{get}\:{thisresult}\:{sor}\:{Tanmay}? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 16/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 18/Jun/18
![from graph attached it is clear that value of xe^(−x) <1 so [xe^(−x) ]=0 when ∞>x≥0](https://www.tinkutara.com/question/Q37775.png)
$${from}\:{graph}\:{attached}\:{it}\:{is}\:{clear}\:{that}\:{value}\:{of} \\ $$$${xe}^{−{x}} <\mathrm{1}\:\:{so}\:\left[{xe}^{−{x}} \right]=\mathrm{0}\:\:{when}\:\:\:\infty>{x}\geqslant\mathrm{0} \\ $$
Commented by abdo.msup.com last updated on 17/Jun/18
![but x e^(−x) <1 ⇏[ x e^(−x) ]=0](https://www.tinkutara.com/question/Q37799.png)
$${but}\:{x}\:{e}^{−{x}} \:<\mathrm{1}\:\nRightarrow\left[\:{x}\:{e}^{−{x}} \right]=\mathrm{0} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18
![do this third bracket [xe^(−x) ] is greatest integer or floor function...if yes then [xe^(−x) ]=0 other wise solve it...](https://www.tinkutara.com/question/Q37807.png)
$${do}\:{this}\:{third}\:{bracket}\:\:\left[{xe}^{−{x}} \right]\:{is}\:{greatest}\:{integer} \\ $$$${or}\:{floor}\:{function}…{if}\:{yes}\:{then}\:\left[{xe}^{−{x}} \right]=\mathrm{0}\: \\ $$$${other}\:{wise}\:{solve}\:{it}… \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18

