Menu Close

let-a-gt-0-find-the-value-of-f-a-0-e-t-2-a-t-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 37635 by math khazana by abdo last updated on 16/Jun/18
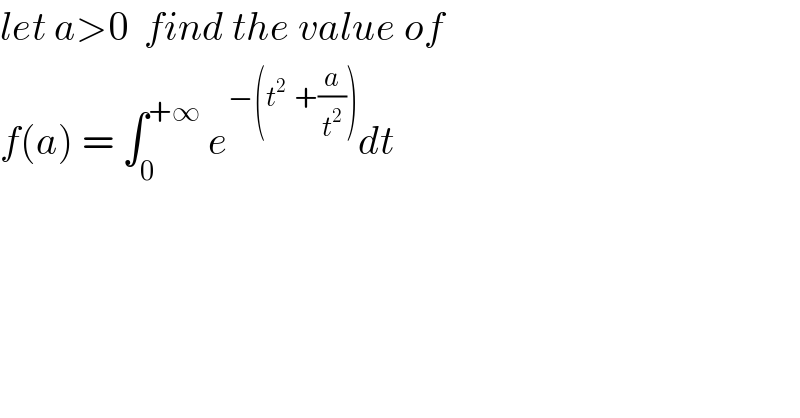
let a>0 find the value of f(a) = ∫_0 ^(+∞) e^(−(t^2 +(a/t^2 ))) dt
$${let}\:{a}>\mathrm{0}\:\:{find}\:{the}\:{value}\:{of}\: \\ $$$${f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{+\infty} \:{e}^{−\left({t}^{\mathrm{2}} \:\:+\frac{{a}}{{t}^{\mathrm{2}} }\right)} {dt}\: \\ $$
Commented by prof Abdo imad last updated on 17/Jun/18
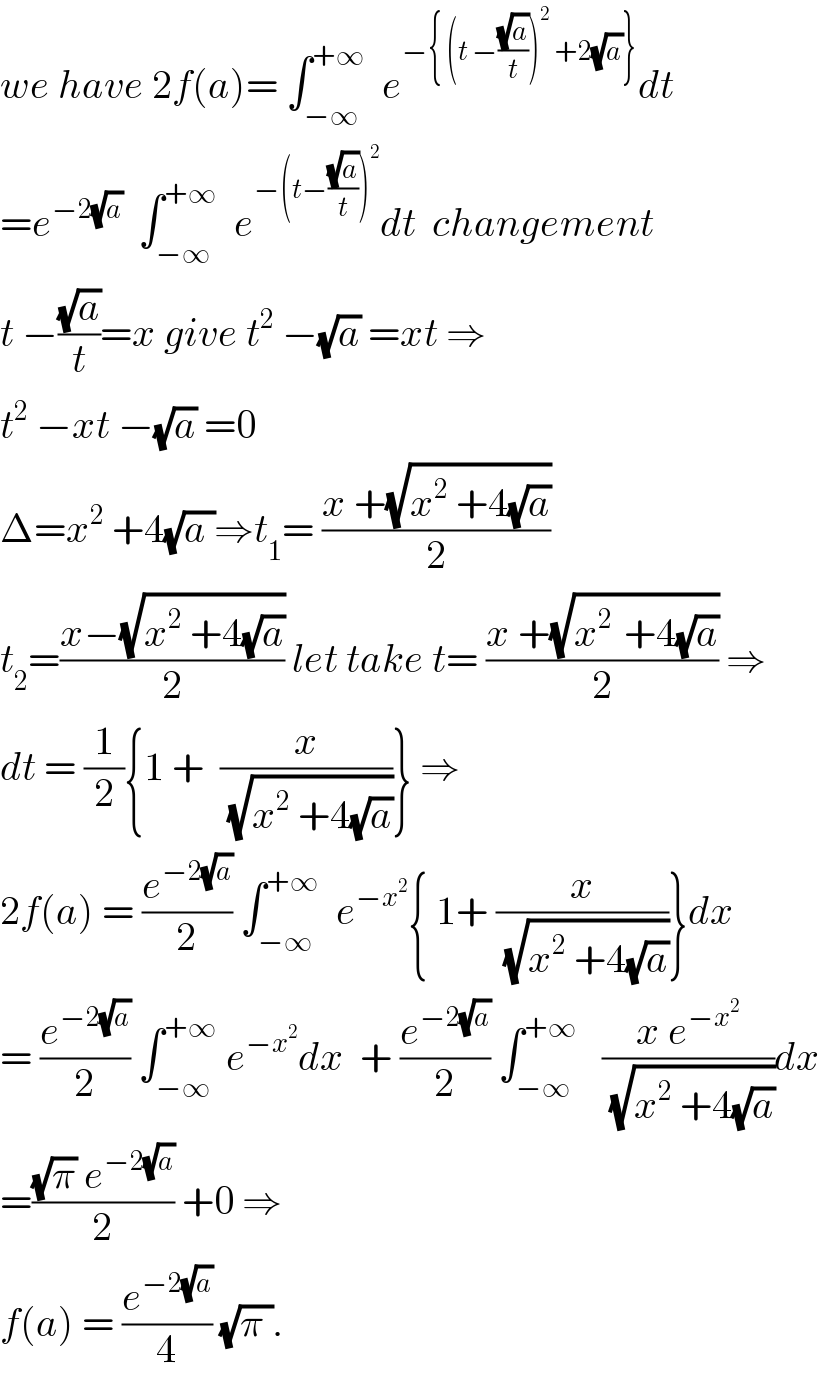
we have 2f(a)= ∫_(−∞) ^(+∞) e^(−{ (t −((√a)/t))^2 +2(√a)}) dt =e^(−2(√a)) ∫_(−∞) ^(+∞) e^(−(t−((√a)/t))^2 ) dt changement t −((√a)/t)=x give t^2 −(√a) =xt ⇒ t^2 −xt −(√a) =0 Δ=x^2 +4(√(a ))⇒t_1 = ((x +(√(x^2 +4(√a))))/2) t_2 =((x−(√(x^2 +4(√a))))/2) let take t= ((x +(√(x^(2 ) +4(√a))))/2) ⇒ dt = (1/2){1 + (x/( (√(x^2 +4(√a)))))} ⇒ 2f(a) = (e^(−2(√a)) /2) ∫_(−∞) ^(+∞) e^(−x^2 ) { 1+ (x/( (√(x^2 +4(√a)))))}dx = (e^(−2(√a)) /2) ∫_(−∞) ^(+∞) e^(−x^2 ) dx + (e^(−2(√a)) /2) ∫_(−∞) ^(+∞) ((x e^(−x^2 ) )/( (√(x^2 +4(√a)))))dx =(((√π) e^(−2(√a)) )/2) +0 ⇒ f(a) = (e^(−2(√a)) /4) (√(π )).
$${we}\:{have}\:\mathrm{2}{f}\left({a}\right)=\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left\{\:\left({t}\:−\frac{\sqrt{{a}}}{{t}}\right)^{\mathrm{2}} \:+\mathrm{2}\sqrt{{a}}\right\}} {dt} \\ $$$$={e}^{−\mathrm{2}\sqrt{{a}}} \:\:\int_{−\infty} ^{+\infty} \:\:{e}^{−\left({t}−\frac{\sqrt{{a}}}{{t}}\right)^{\mathrm{2}} } {dt}\:\:{changement} \\ $$$${t}\:−\frac{\sqrt{{a}}}{{t}}={x}\:{give}\:{t}^{\mathrm{2}} \:−\sqrt{{a}}\:={xt}\:\Rightarrow \\ $$$${t}^{\mathrm{2}} \:−{xt}\:−\sqrt{{a}}\:=\mathrm{0} \\ $$$$\Delta={x}^{\mathrm{2}} \:+\mathrm{4}\sqrt{{a}\:}\Rightarrow{t}_{\mathrm{1}} =\:\frac{{x}\:+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}\sqrt{{a}}}}{\mathrm{2}} \\ $$$${t}_{\mathrm{2}} =\frac{{x}−\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}\sqrt{{a}}}}{\mathrm{2}}\:{let}\:{take}\:{t}=\:\frac{{x}\:+\sqrt{{x}^{\mathrm{2}\:} \:+\mathrm{4}\sqrt{{a}}}}{\mathrm{2}}\:\Rightarrow \\ $$$${dt}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{1}\:+\:\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}\sqrt{{a}}}}\right\}\:\Rightarrow \\ $$$$\mathrm{2}{f}\left({a}\right)\:=\:\frac{{e}^{−\mathrm{2}\sqrt{{a}}} }{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:{e}^{−{x}^{\mathrm{2}} } \left\{\:\mathrm{1}+\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}\sqrt{{a}}}}\right\}{dx} \\ $$$$=\:\frac{{e}^{−\mathrm{2}\sqrt{{a}}} }{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:{e}^{−{x}^{\mathrm{2}} } {dx}\:\:+\:\frac{{e}^{−\mathrm{2}\sqrt{{a}}} }{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{x}\:{e}^{−{x}^{\mathrm{2}} } }{\:\sqrt{{x}^{\mathrm{2}} \:+\mathrm{4}\sqrt{{a}}}}{dx} \\ $$$$=\frac{\sqrt{\pi}\:{e}^{−\mathrm{2}\sqrt{{a}}} }{\mathrm{2}}\:+\mathrm{0}\:\Rightarrow \\ $$$${f}\left({a}\right)\:=\:\frac{{e}^{−\mathrm{2}\sqrt{{a}}} }{\mathrm{4}}\:\sqrt{\pi\:}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *