Question Number 37636 by math khazana by abdo last updated on 16/Jun/18
![find ∫_0 ^6 (x^2 −x+1)e^([−2x]) dx .](https://www.tinkutara.com/question/Q37636.png)
$${find}\:\:\int_{\mathrm{0}} ^{\mathrm{6}} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right){e}^{\left[−\mathrm{2}{x}\right]} {dx}\:. \\ $$
Commented by prof Abdo imad last updated on 16/Jun/18
![let A = ∫_0 ^6 (x^2 −x+1)e^([−2x]) dx A=_(2x=t) ∫_0 ^(12) ( (t^2 /4) −(t/2) +1)e^([−t]) (dt/2) = (1/8) ∫_0 ^(12) ( t^2 −2t +4) e^([−t]) dt 8A= Σ_(k=0) ^(11) ∫_k ^(k+1) (t^2 −2t +4)e^(−k) dt =Σ_(k=0) ^(11) e^(−k) ∫_k ^(k+1) (t^2 −2t +4)dt=Σ_(k=0) ^(11) e^(−k) T_k T_k = ∫_k ^(k+1) (t^2 −2t +4)dt=[(t^3 /3) −t^2 +4t]_k ^(k+1) =(((k+1)^3 )/3) −(k+1)^2 +4(k+1)−(k^3 /3) +k^2 −4k =((k^3 +3k^2 +3k +1 −k^3 )/3) −k^2 −2k −1 +k^2 +4 =k^2 +k +(1/3) −2k +3 =k^2 −k +((10)/3) ⇒8A= Σ_(k=0) ^(11) e^(−k) {k^2 −k +((10)/3)} A =(1/8)Σ_(k=0) ^(11) ( k^2 −k +((10)/3)) e^(−k) .](https://www.tinkutara.com/question/Q37708.png)
$${let}\:{A}\:=\:\int_{\mathrm{0}} ^{\mathrm{6}} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right){e}^{\left[−\mathrm{2}{x}\right]} {dx} \\ $$$${A}=_{\mathrm{2}{x}={t}} \:\:\int_{\mathrm{0}} ^{\mathrm{12}} \left(\:\frac{{t}^{\mathrm{2}} }{\mathrm{4}}\:−\frac{{t}}{\mathrm{2}}\:+\mathrm{1}\right){e}^{\left[−{t}\right]} \:\frac{{dt}}{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\mathrm{12}} \left(\:{t}^{\mathrm{2}} \:−\mathrm{2}{t}\:+\mathrm{4}\right)\:{e}^{\left[−{t}\right]} {dt} \\ $$$$\mathrm{8}{A}=\:\sum_{{k}=\mathrm{0}} ^{\mathrm{11}} \:\int_{{k}} ^{{k}+\mathrm{1}} \left({t}^{\mathrm{2}} \:−\mathrm{2}{t}\:+\mathrm{4}\right){e}^{−{k}} {dt} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\mathrm{11}} \:{e}^{−{k}} \:\:\int_{{k}} ^{{k}+\mathrm{1}} \left({t}^{\mathrm{2}} −\mathrm{2}{t}\:+\mathrm{4}\right){dt}=\sum_{{k}=\mathrm{0}} ^{\mathrm{11}} {e}^{−{k}} \:{T}_{{k}} \\ $$$${T}_{{k}} =\:\int_{{k}} ^{{k}+\mathrm{1}} \left({t}^{\mathrm{2}} \:−\mathrm{2}{t}\:+\mathrm{4}\right){dt}=\left[\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\:−{t}^{\mathrm{2}} \:+\mathrm{4}{t}\right]_{{k}} ^{{k}+\mathrm{1}} \\ $$$$=\frac{\left({k}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}}\:−\left({k}+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{4}\left({k}+\mathrm{1}\right)−\frac{{k}^{\mathrm{3}} }{\mathrm{3}}\:+{k}^{\mathrm{2}} \:−\mathrm{4}{k} \\ $$$$=\frac{{k}^{\mathrm{3}} \:+\mathrm{3}{k}^{\mathrm{2}} \:+\mathrm{3}{k}\:+\mathrm{1}\:−{k}^{\mathrm{3}} }{\mathrm{3}}\:−{k}^{\mathrm{2}} \:−\mathrm{2}{k}\:−\mathrm{1}\:+{k}^{\mathrm{2}} \:+\mathrm{4} \\ $$$$={k}^{\mathrm{2}} \:+{k}\:+\frac{\mathrm{1}}{\mathrm{3}}\:−\mathrm{2}{k}\:+\mathrm{3} \\ $$$$={k}^{\mathrm{2}} \:−{k}\:+\frac{\mathrm{10}}{\mathrm{3}}\:\Rightarrow\mathrm{8}{A}=\:\sum_{{k}=\mathrm{0}} ^{\mathrm{11}} \:{e}^{−{k}} \left\{{k}^{\mathrm{2}} −{k}\:+\frac{\mathrm{10}}{\mathrm{3}}\right\} \\ $$$${A}\:=\frac{\mathrm{1}}{\mathrm{8}}\sum_{{k}=\mathrm{0}} ^{\mathrm{11}} \left(\:{k}^{\mathrm{2}} −{k}\:+\frac{\mathrm{10}}{\mathrm{3}}\right)\:{e}^{−{k}} \:\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18
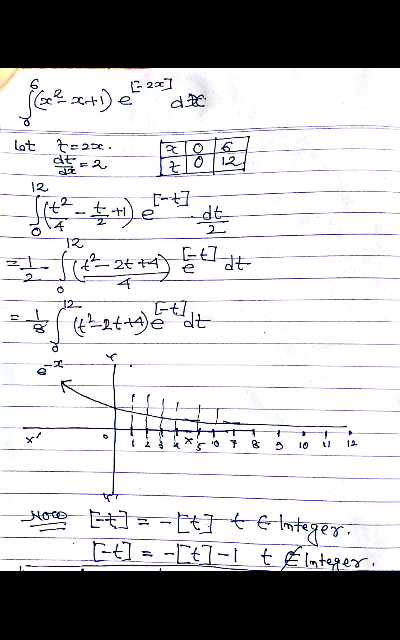
Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18

Commented by tanmay.chaudhury50@gmail.com last updated on 17/Jun/18

