Question Number 103236 by Dwaipayan Shikari last updated on 13/Jul/20

$${e}^{{e}^{{e}…..\infty} } =? \\ $$
Commented by Dwaipayan Shikari last updated on 13/Jul/20

$${e}^{{e}^{{e}^{{e}^{{e}^{……….} } } } } ={y} \\ $$$${e}^{{y}} ={y} \\ $$$${e}^{−{y}} =\frac{\mathrm{1}}{{y}} \\ $$$$−{ye}^{−{y}} =−\mathrm{1} \\ $$$$−{y}={W}_{\mathrm{0}} \left(−\mathrm{1}\right) \\ $$$${y}=−{W}_{\mathrm{0}} \left(−\mathrm{1}\right)=\mathrm{0}.\mathrm{3181}−\mathrm{1}.\mathrm{333}{i} \\ $$
Commented by mr W last updated on 13/Jul/20

$$=\infty \\ $$
Commented by mr W last updated on 13/Jul/20
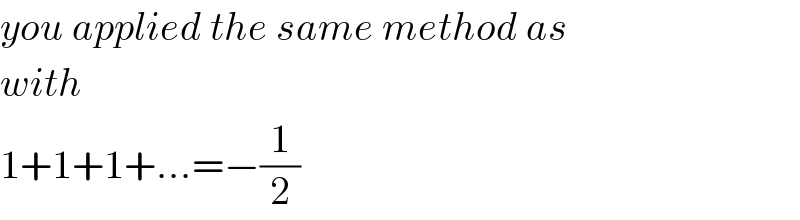
$${you}\:{applied}\:{the}\:{same}\:{method}\:{as} \\ $$$${with} \\ $$$$\mathrm{1}+\mathrm{1}+\mathrm{1}+…=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
