Question Number 168878 by bounhome last updated on 20/Apr/22
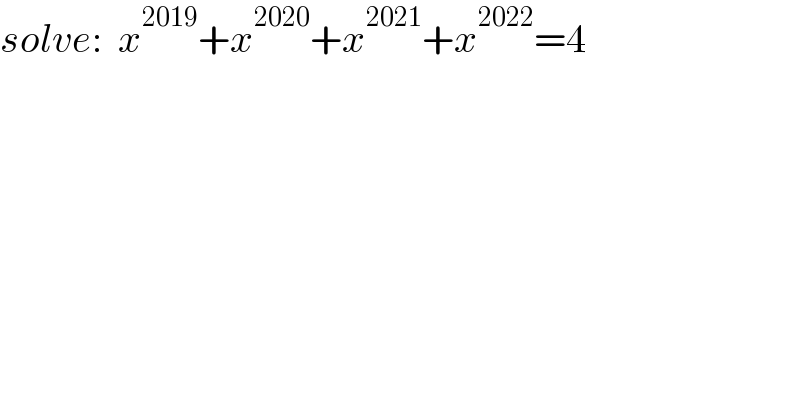
$${solve}:\:\:{x}^{\mathrm{2019}} +{x}^{\mathrm{2020}} +{x}^{\mathrm{2021}} +{x}^{\mathrm{2022}} =\mathrm{4} \\ $$
Commented by bagjagugum123 last updated on 20/Apr/22

$${x}=\mathrm{1} \\ $$
Commented by mathlove last updated on 20/Apr/22
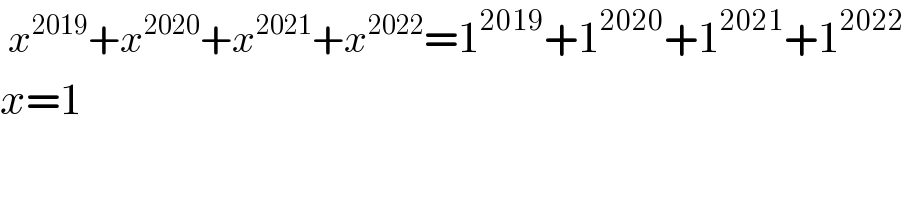
$$\:{x}^{\mathrm{2019}} +{x}^{\mathrm{2020}} +{x}^{\mathrm{2021}} +{x}^{\mathrm{2022}} =\mathrm{1}^{\mathrm{2019}} +\mathrm{1}^{\mathrm{2020}} +\mathrm{1}^{\mathrm{2021}} +\mathrm{1}^{\mathrm{2022}} \\ $$$${x}=\mathrm{1} \\ $$
Commented by MJS_new last updated on 20/Apr/22

$${x}=\mathrm{1} \\ $$$${x}\approx−\mathrm{1}.\mathrm{0031931511975} \\ $$$$\mathrm{and}\:\mathrm{2020}\:\mathrm{complex}\:\mathrm{solutions} \\ $$
Answered by Rasheed.Sindhi last updated on 20/Apr/22
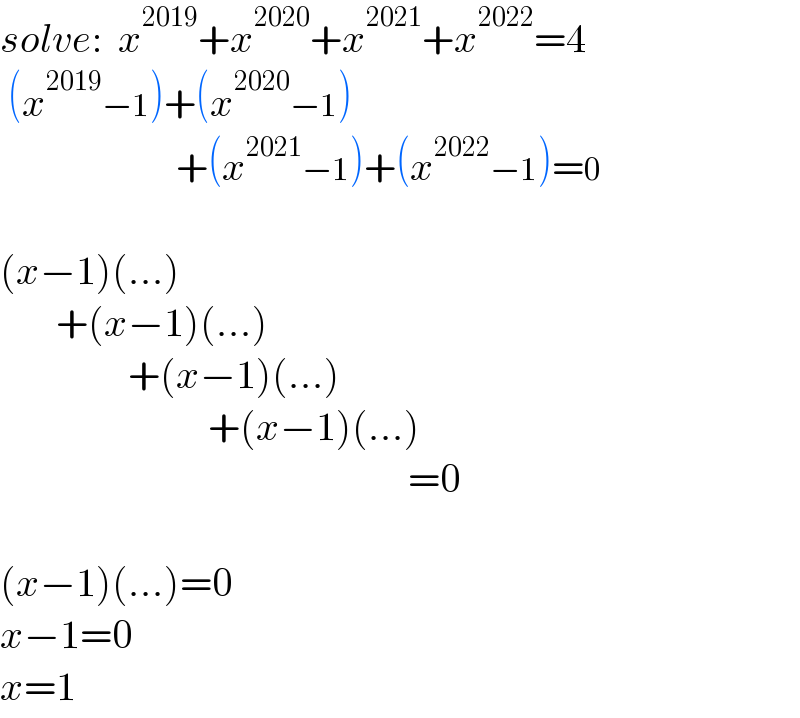
$${solve}:\:\:{x}^{\mathrm{2019}} +{x}^{\mathrm{2020}} +{x}^{\mathrm{2021}} +{x}^{\mathrm{2022}} =\mathrm{4} \\ $$$$\:\left({x}^{\mathrm{2019}} −\mathrm{1}\right)+\left({x}^{\mathrm{2020}} −\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({x}^{\mathrm{2021}} −\mathrm{1}\right)+\left({x}^{\mathrm{2022}} −\mathrm{1}\right)=\mathrm{0} \\ $$$$ \\ $$$$\left({x}−\mathrm{1}\right)\left(…\right) \\ $$$$\:\:\:\:\:\:\:+\left({x}−\mathrm{1}\right)\left(…\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({x}−\mathrm{1}\right)\left(…\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left({x}−\mathrm{1}\right)\left(…\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{0} \\ $$$$ \\ $$$$\left({x}−\mathrm{1}\right)\left(…\right)=\mathrm{0} \\ $$$${x}−\mathrm{1}=\mathrm{0} \\ $$$${x}=\mathrm{1} \\ $$
Commented by mathlove last updated on 20/Apr/22

$${nice} \\ $$
