Question Number 37818 by prof Abdo imad last updated on 17/Jun/18
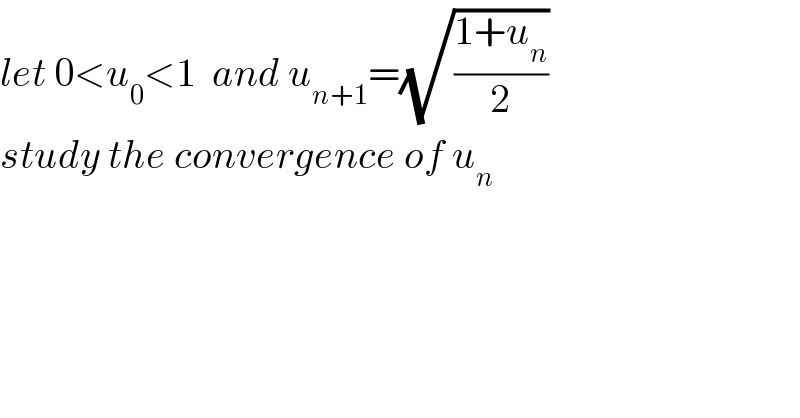
$${let}\:\mathrm{0}<{u}_{\mathrm{0}} <\mathrm{1}\:\:{and}\:{u}_{{n}+\mathrm{1}} =\sqrt{\frac{\mathrm{1}+{u}_{{n}} }{\mathrm{2}}} \\ $$$${study}\:{the}\:{convergence}\:{of}\:{u}_{{n}} \: \\ $$$$ \\ $$
Commented by math khazana by abdo last updated on 19/Jun/18

$${let}\:{f}\left({x}\right)\:=\sqrt{\frac{\mathrm{1}+{x}}{\mathrm{2}}}\:\:{with}\:{x}\geqslant\mathrm{0}\: \\ $$$${f}\left({x}\right)={x}\:\Rightarrow\frac{\mathrm{1}+{x}}{\mathrm{2}}\:={x}^{\mathrm{2}} \:\Rightarrow\mathrm{1}+{x}\:=\mathrm{2}{x}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{2}{x}^{\mathrm{2}} −{x}−\mathrm{1}\:=\mathrm{0}\:\:\:\Delta\:=\mathrm{1}+\mathrm{8}\:=\mathrm{9} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{3}}{\mathrm{4}}\:=\mathrm{1}\:\:{and}\:{x}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{3}}{\mathrm{4}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\:{we}\:{have} \\ $$$${u}_{{n}+\mathrm{1}} ={f}\left({u}_{{n}} \right)\:{and}\:{f}\:{is}\:{continue}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} {u}_{{n}} =\mathrm{1} \\ $$$${let}\:{find}\:{another}\:{form}\:{of}\:{u}_{{n}} \:{we}\:{put} \\ $$$${u}_{\mathrm{0}} ={cos}\alpha\:\:\Rightarrow\:{u}_{\mathrm{1}} =\sqrt{\frac{\mathrm{1}+{cos}\left(\alpha\right)}{\mathrm{2}}}\:\:={cos}\left(\frac{\alpha}{\mathrm{2}}\right) \\ $$$$\:{let}\:{prove}\:{that}\:{u}_{{n}} =\:{cos}\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right) \\ $$$${relation}\:{true}\:{for}\:{n}=\mathrm{0} \\ $$$${let}\:{suppose}\:{u}_{{n}} ={cos}\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)\:\Rightarrow \\ $$$${u}_{{n}+\mathrm{1}} =\sqrt{\frac{\mathrm{1}+{u}_{{n}} }{\mathrm{2}}}\:=\sqrt{\frac{\mathrm{1}+{cos}\left(\frac{\alpha}{\mathrm{2}^{{n}} }\right)}{\mathrm{2}}} \\ $$$$={cos}\left(\frac{\alpha}{\mathrm{2}^{{n}+\mathrm{1}} }\right)\:.\:{its}\:{now}\:{clear}\:{that} \\ $$$${lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} =\mathrm{1}\:. \\ $$
