Menu Close

let-f-x-x-2-1-x-4-1-calculate-f-n-x-2-find-f-n-0-3-developp-f-at-integr-serie-4-calculate-0-1-f-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 37820 by prof Abdo imad last updated on 17/Jun/18
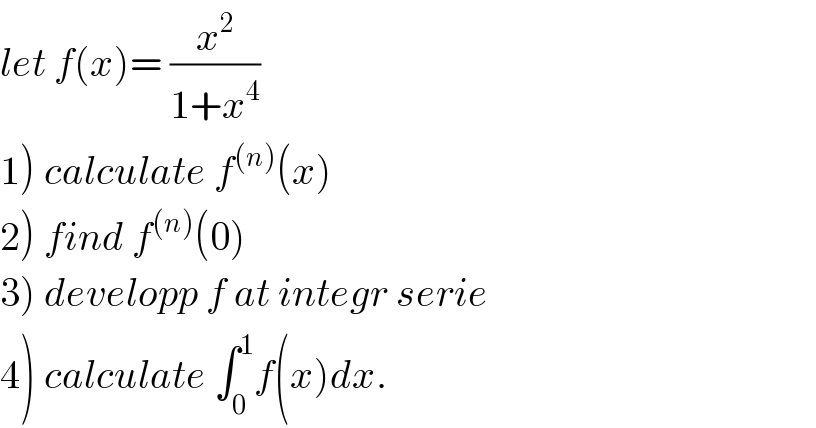
let f(x)= (x^2 /(1+x^4 )) 1) calculate f^((n)) (x) 2) find f^((n)) (0) 3) developp f at integr serie 4) calculate ∫_0 ^1 f(x)dx.
$${let}\:{f}\left({x}\right)=\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{4}} } \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{f}^{\left({n}\right)} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{f}^{\left({n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{3}\right)\:{developp}\:{f}\:{at}\:{integr}\:{serie} \\ $$$$\left.\mathrm{4}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}. \\ $$
Commented by prof Abdo imad last updated on 18/Jun/18
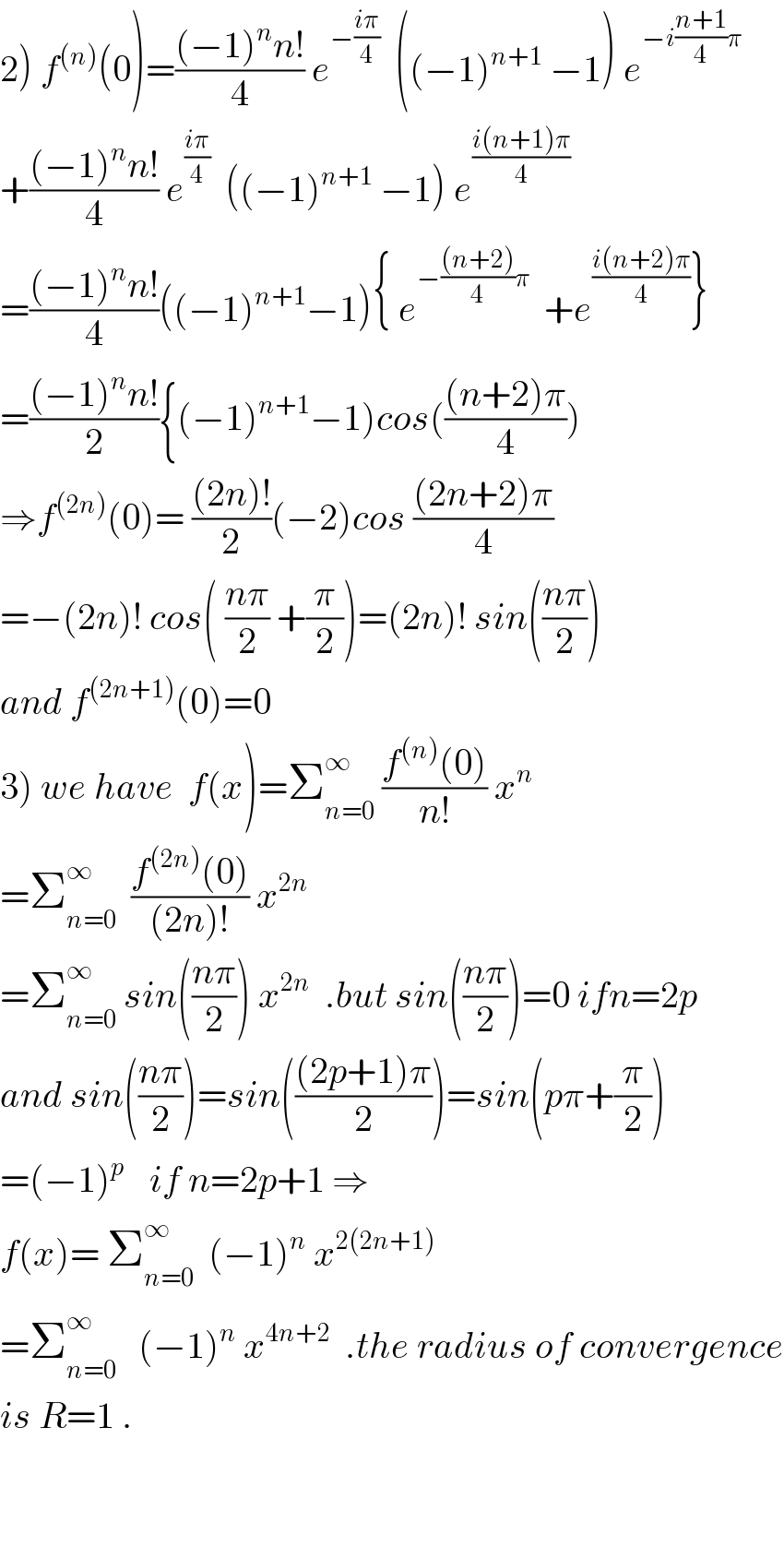
2) f^((n)) (0)=(((−1)^n n!)/4) e^(−((iπ)/4)) ((−1)^(n+1) −1) e^(−i((n+1)/4)π) +(((−1)^n n!)/4) e^((iπ)/4) ((−1)^(n+1) −1) e^((i(n+1)π)/4) =(((−1)^n n!)/4)((−1)^(n+1) −1){ e^(−(((n+2))/4)π) +e^((i(n+2)π)/4) } =(((−1)^n n!)/2){(−1)^(n+1) −1)cos((((n+2)π)/4)) ⇒f^((2n)) (0)= (((2n)!)/2)(−2)cos (((2n+2)π)/4) =−(2n)! cos( ((nπ)/2) +(π/2))=(2n)! sin(((nπ)/2)) and f^((2n+1)) (0)=0 3) we have f(x)=Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n =Σ_(n=0) ^∞ ((f^((2n)) (0))/((2n)!)) x^(2n) =Σ_(n=0) ^∞ sin(((nπ)/2)) x^(2n) .but sin(((nπ)/2))=0 ifn=2p and sin(((nπ)/2))=sin((((2p+1)π)/2))=sin(pπ+(π/2)) =(−1)^(p ) if n=2p+1 ⇒ f(x)= Σ_(n=0) ^∞ (−1)^n x^(2(2n+1)) =Σ_(n=0) ^∞ (−1)^n x^(4n+2) .the radius of convergence is R=1 .
$$\left.\mathrm{2}\right)\:{f}^{\left({n}\right)} \left(\mathrm{0}\right)=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\mathrm{4}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:\left(\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:−\mathrm{1}\right)\:{e}^{−{i}\frac{{n}+\mathrm{1}}{\mathrm{4}}\pi} \\ $$$$+\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\mathrm{4}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:\left(\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \:−\mathrm{1}\right)\:{e}^{\frac{{i}\left({n}+\mathrm{1}\right)\pi}{\mathrm{4}}} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\mathrm{4}}\left(\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} −\mathrm{1}\right)\left\{\:{e}^{−\frac{\left({n}+\mathrm{2}\right)}{\mathrm{4}}\pi} \:\:+{e}^{\frac{{i}\left({n}+\mathrm{2}\right)\pi}{\mathrm{4}}} \right\} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\mathrm{2}}\left\{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} −\mathrm{1}\right){cos}\left(\frac{\left({n}+\mathrm{2}\right)\pi}{\mathrm{4}}\right) \\ $$$$\Rightarrow{f}^{\left(\mathrm{2}{n}\right)} \left(\mathrm{0}\right)=\:\frac{\left(\mathrm{2}{n}\right)!}{\mathrm{2}}\left(−\mathrm{2}\right){cos}\:\frac{\left(\mathrm{2}{n}+\mathrm{2}\right)\pi}{\mathrm{4}} \\ $$$$=−\left(\mathrm{2}{n}\right)!\:{cos}\left(\:\frac{{n}\pi}{\mathrm{2}}\:+\frac{\pi}{\mathrm{2}}\right)=\left(\mathrm{2}{n}\right)!\:{sin}\left(\frac{{n}\pi}{\mathrm{2}}\right) \\ $$$${and}\:{f}^{\left(\mathrm{2}{n}+\mathrm{1}\right)} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\left.\mathrm{3}\right)\:{we}\:{have}\:\:{f}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}\:{x}^{{n}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{f}^{\left(\mathrm{2}{n}\right)} \left(\mathrm{0}\right)}{\left(\mathrm{2}{n}\right)!}\:{x}^{\mathrm{2}{n}} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:{sin}\left(\frac{{n}\pi}{\mathrm{2}}\right)\:{x}^{\mathrm{2}{n}} \:\:.{but}\:{sin}\left(\frac{{n}\pi}{\mathrm{2}}\right)=\mathrm{0}\:{ifn}=\mathrm{2}{p} \\ $$$${and}\:{sin}\left(\frac{{n}\pi}{\mathrm{2}}\right)={sin}\left(\frac{\left(\mathrm{2}{p}+\mathrm{1}\right)\pi}{\mathrm{2}}\right)={sin}\left({p}\pi+\frac{\pi}{\mathrm{2}}\right) \\ $$$$=\left(−\mathrm{1}\right)^{{p}\:\:\:} \:\:{if}\:{n}=\mathrm{2}{p}+\mathrm{1}\:\Rightarrow \\ $$$${f}\left({x}\right)=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{4}{n}+\mathrm{2}} \:\:.{the}\:{radius}\:{of}\:{convergence} \\ $$$${is}\:{R}=\mathrm{1}\:. \\ $$$$ \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 18/Jun/18
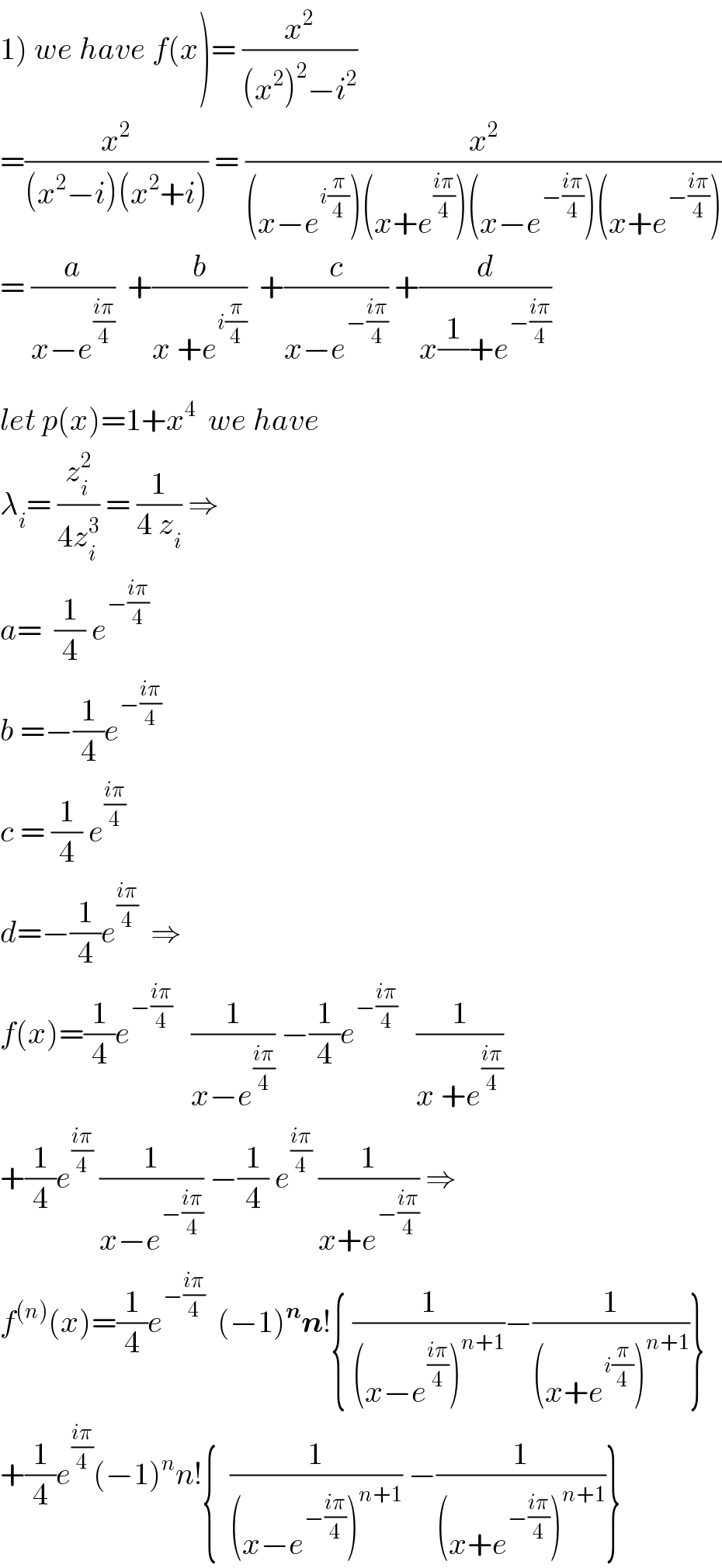
1) we have f(x)= (x^2 /((x^2 )^2 −i^2 )) =(x^2 /((x^2 −i)(x^2 +i))) = (x^2 /((x−e^(i(π/4)) )(x+e^((iπ)/4) )(x−e^(−((iπ)/4)) )(x+e^(−((iπ)/4)) ))) = (a/(x−e^((iπ)/4) )) +(b/(x +e^(i(π/4)) )) +(c/(x−e^(−((iπ)/4)) )) +(d/(x(1/)+e^(−((iπ)/4)) )) let p(x)=1+x^4 we have λ_i = (z_i ^2 /(4z_i ^3 )) = (1/(4 z_i )) ⇒ a= (1/4) e^(−((iπ)/4)) b =−(1/4)e^(−((iπ)/4)) c = (1/4) e^((iπ)/4) d=−(1/4)e^((iπ)/4) ⇒ f(x)=(1/4)e^(−((iπ)/4)) (1/(x−e^((iπ)/4) )) −(1/4)e^(−((iπ)/4)) (1/(x +e^((iπ)/4) )) +(1/4)e^((iπ)/4) (1/(x−e^(−((iπ)/4)) )) −(1/4) e^((iπ)/4) (1/(x+e^(−((iπ)/4)) )) ⇒ f^((n)) (x)=(1/4)e^(−((iπ)/4)) (−1)^n n!{ (1/((x−e^((iπ)/4) )^(n+1) ))−(1/((x+e^(i(π/4)) )^(n+1) ))} +(1/4)e^((iπ)/4) (−1)^n n!{ (1/((x−e^(−((iπ)/4)) )^(n+1) )) −(1/((x+e^(−((iπ)/4)) )^(n+1) ))}
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{f}\left({x}\right)=\:\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} \right)^{\mathrm{2}} −{i}^{\mathrm{2}} } \\ $$$$=\frac{{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} −{i}\right)\left({x}^{\mathrm{2}} +{i}\right)}\:=\:\frac{{x}^{\mathrm{2}} }{\left({x}−{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)\left({x}+{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\left({x}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)\left({x}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)} \\ $$$$=\:\frac{{a}}{{x}−{e}^{\frac{{i}\pi}{\mathrm{4}}} }\:\:+\frac{{b}}{{x}\:+{e}^{{i}\frac{\pi}{\mathrm{4}}} }\:\:+\frac{{c}}{{x}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} }\:+\frac{{d}}{{x}\frac{\mathrm{1}}{}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} } \\ $$$${let}\:{p}\left({x}\right)=\mathrm{1}+{x}^{\mathrm{4}} \:\:{we}\:{have} \\ $$$$\lambda_{{i}} =\:\frac{{z}_{{i}} ^{\mathrm{2}} }{\mathrm{4}{z}_{{i}} ^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{4}\:{z}_{{i}} }\:\Rightarrow \\ $$$${a}=\:\:\frac{\mathrm{1}}{\mathrm{4}}\:{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$${b}\:=−\frac{\mathrm{1}}{\mathrm{4}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \\ $$$${c}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \\ $$$${d}=−\frac{\mathrm{1}}{\mathrm{4}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:\:\frac{\mathrm{1}}{{x}−{e}^{\frac{{i}\pi}{\mathrm{4}}} }\:−\frac{\mathrm{1}}{\mathrm{4}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:\:\frac{\mathrm{1}}{{x}\:+{e}^{\frac{{i}\pi}{\mathrm{4}}} } \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\frac{\mathrm{1}}{{x}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} }\:−\frac{\mathrm{1}}{\mathrm{4}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\frac{\mathrm{1}}{{x}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} }\:\Rightarrow \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}{e}^{−\frac{{i}\pi}{\mathrm{4}}} \:\:\left(−\mathrm{1}\right)^{\boldsymbol{{n}}} \boldsymbol{{n}}!\left\{\:\frac{\mathrm{1}}{\left({x}−{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}+\mathrm{1}} }−\frac{\mathrm{1}}{\left({x}+{e}^{{i}\frac{\pi}{\mathrm{4}}} \right)^{{n}+\mathrm{1}} }\right\} \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \left(−\mathrm{1}\right)^{{n}} {n}!\left\{\:\:\frac{\mathrm{1}}{\left({x}−{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}+\mathrm{1}} }\:−\frac{\mathrm{1}}{\left({x}+{e}^{−\frac{{i}\pi}{\mathrm{4}}} \right)^{{n}+\mathrm{1}} }\right\} \\ $$
Answered by behi83417@gmail.com last updated on 18/Jun/18
f(x)=(1/2).((2x^2 )/((x^2 +i)(x^2 −i)))=(1/2).(((x^2 +i)+(x^2 −i))/((x^2 +i)(x^2 −i)))= =(1/2)[(1/(x^2 +i))+(1/(x^2 −i))]=(1/2)[(1/((x+i(√i))(x−i(√i))))+ +(1/((x−(√i))(x+(√i))))]=(1/2)[(1/(2i(√i)))[(((x+i(√i))−(x−i(√i)))/((x+i(√i))(x−i(√i))))]+ +[(1/(2(√i)))[(((x+(√i))−(x−(√i)))/((x+(√i))(x−(√i))))]]=^((√i)=a) =−(a/4)[(1/(x−a^3 ))−(1/(x+a^3 ))+(i/(x−a))−(i/(x+a))] f^1 (x)=−(a/4)[((−1)/((x−a^3 )^2 ))+(1/((x+a^3 )^2 ))−(i/((x+a)^2 ))+(i/((x−a)^2 ))] f^n (x)=((n!a(−1)^n )/4)[(1/((x−a^3 )^(n+1) ))−(1/((x−a^3 )^(n+1) ))+ +(i/((x−a)^(n+1) ))−(i/((x−a)^(n+1) ))] . 2)f^n (0)=0 4)∫((x^2 dx)/(1+x^4 ))=−(a/4)[ln((x+a^3 )/(x−a^3 ))+i.ln((x+a)/(x−a))] F(1)=−(a/4)[ln((1+a^3 )/(1−a^3 ))+i.ln((1+a)/(1−a))]= −((√i)/4)[i(√i)+(√i)−i+i(i(√i)+(√i)+i)]= =−((√i)/4)[i(√i)+(√i)−i−(√i)+i(√i)−1]= =−((√i)/4)[2i(√i)−i−1]=−(1/4)(−2−i(√i)−(√i)) F(0)=−(a/4)[ln(−1)+i.ln(−1)]= =−(a/4)(((iπ)/2)+i.((iπ)/2))=−((π(√i))/8)(i−1)=((π(√i))/8)(1−i). I=F(1)−F(0)=(1/8)[4+(i+1)(√i)+π(√i)(i−1)]. i=cos(π/2)+isin(π/2)=e^((iπ)/2) ⇒(√i)=e^((iπ)/4) ((1+a^3 )/(1−a^3 ))=(((1+a^3 )^2 )/(1−a^6 ))=(((1+2i(√i)−i))/(1+i)).((1−i)/(1−i))= =(1/2)(1−i+2i(√i)+2(√i)−i−1)=i(√i)+(√i)−i ((1+a)/(1−a))=(((1+a)^2 )/(1−a^2 ))=((1+2(√i)+i)/(1−i)).((1+i)/(1+i))= =(1/2)(1+i+2(√i)+2i(√i)+i−1)=i(√i)+(√i)+i
$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +{i}\right)\left({x}^{\mathrm{2}} −{i}\right)}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\left({x}^{\mathrm{2}} +{i}\right)+\left({x}^{\mathrm{2}} −{i}\right)}{\left({x}^{\mathrm{2}} +{i}\right)\left({x}^{\mathrm{2}} −{i}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{i}}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{i}}\right]=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\left({x}+{i}\sqrt{{i}}\right)\left({x}−{i}\sqrt{{i}}\right)}+\right. \\ $$$$\left.+\frac{\mathrm{1}}{\left({x}−\sqrt{{i}}\right)\left({x}+\sqrt{{i}}\right)}\right]=\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{{i}}}\left[\frac{\left({x}+{i}\sqrt{{i}}\right)−\left({x}−{i}\sqrt{{i}}\right)}{\left({x}+{i}\sqrt{{i}}\right)\left({x}−{i}\sqrt{{i}}\right)}\right]+\right. \\ $$$$+\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{{i}}}\left[\frac{\left({x}+\sqrt{{i}}\right)−\left({x}−\sqrt{{i}}\right)}{\left({x}+\sqrt{{i}}\right)\left({x}−\sqrt{{i}}\right)}\right]\right]\overset{\sqrt{{i}}={a}} {=} \\ $$$$=−\frac{{a}}{\mathrm{4}}\left[\frac{\mathrm{1}}{{x}−{a}^{\mathrm{3}} }−\frac{\mathrm{1}}{{x}+{a}^{\mathrm{3}} }+\frac{{i}}{{x}−{a}}−\frac{{i}}{{x}+{a}}\right] \\ $$$${f}^{\mathrm{1}} \left({x}\right)=−\frac{{a}}{\mathrm{4}}\left[\frac{−\mathrm{1}}{\left({x}−{a}^{\mathrm{3}} \right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}+{a}^{\mathrm{3}} \right)^{\mathrm{2}} }−\frac{{i}}{\left({x}+{a}\right)^{\mathrm{2}} }+\frac{{i}}{\left({x}−{a}\right)^{\mathrm{2}} }\right] \\ $$$${f}^{{n}} \left({x}\right)=\frac{{n}!{a}\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}}\left[\frac{\mathrm{1}}{\left({x}−{a}^{\mathrm{3}} \right)^{{n}+\mathrm{1}} }−\frac{\mathrm{1}}{\left({x}−{a}^{\mathrm{3}} \right)^{{n}+\mathrm{1}} }+\right. \\ $$$$\left.+\frac{{i}}{\left({x}−{a}\right)^{{n}+\mathrm{1}} }−\frac{{i}}{\left({x}−{a}\right)^{{n}+\mathrm{1}} }\right]\:. \\ $$$$\left.\mathrm{2}\right){f}^{{n}} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\left.\mathrm{4}\right)\int\frac{{x}^{\mathrm{2}} {dx}}{\mathrm{1}+{x}^{\mathrm{4}} }=−\frac{{a}}{\mathrm{4}}\left[{ln}\frac{{x}+{a}^{\mathrm{3}} }{{x}−{a}^{\mathrm{3}} }+{i}.{ln}\frac{{x}+{a}}{{x}−{a}}\right] \\ $$$${F}\left(\mathrm{1}\right)=−\frac{{a}}{\mathrm{4}}\left[{ln}\frac{\mathrm{1}+{a}^{\mathrm{3}} }{\mathrm{1}−{a}^{\mathrm{3}} }+{i}.{ln}\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}\right]= \\ $$$$−\frac{\sqrt{{i}}}{\mathrm{4}}\left[{i}\sqrt{{i}}+\sqrt{{i}}−{i}+{i}\left({i}\sqrt{{i}}+\sqrt{{i}}+{i}\right)\right]= \\ $$$$=−\frac{\sqrt{{i}}}{\mathrm{4}}\left[{i}\sqrt{{i}}+\sqrt{{i}}−{i}−\sqrt{{i}}+{i}\sqrt{{i}}−\mathrm{1}\right]= \\ $$$$=−\frac{\sqrt{{i}}}{\mathrm{4}}\left[\mathrm{2}{i}\sqrt{{i}}−{i}−\mathrm{1}\right]=−\frac{\mathrm{1}}{\mathrm{4}}\left(−\mathrm{2}−{i}\sqrt{{i}}−\sqrt{{i}}\right) \\ $$$${F}\left(\mathrm{0}\right)=−\frac{{a}}{\mathrm{4}}\left[{ln}\left(−\mathrm{1}\right)+{i}.{ln}\left(−\mathrm{1}\right)\right]= \\ $$$$=−\frac{{a}}{\mathrm{4}}\left(\frac{{i}\pi}{\mathrm{2}}+{i}.\frac{{i}\pi}{\mathrm{2}}\right)=−\frac{\pi\sqrt{{i}}}{\mathrm{8}}\left({i}−\mathrm{1}\right)=\frac{\pi\sqrt{{i}}}{\mathrm{8}}\left(\mathrm{1}−{i}\right). \\ $$$${I}={F}\left(\mathrm{1}\right)−{F}\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{8}}\left[\mathrm{4}+\left({i}+\mathrm{1}\right)\sqrt{{i}}+\pi\sqrt{{i}}\left({i}−\mathrm{1}\right)\right]. \\ $$$${i}={cos}\frac{\pi}{\mathrm{2}}+{isin}\frac{\pi}{\mathrm{2}}={e}^{\frac{{i}\pi}{\mathrm{2}}} \Rightarrow\sqrt{{i}}={e}^{\frac{{i}\pi}{\mathrm{4}}} \\ $$$$\frac{\mathrm{1}+{a}^{\mathrm{3}} }{\mathrm{1}−{a}^{\mathrm{3}} }=\frac{\left(\mathrm{1}+{a}^{\mathrm{3}} \right)^{\mathrm{2}} }{\mathrm{1}−{a}^{\mathrm{6}} }=\frac{\left(\mathrm{1}+\mathrm{2}{i}\sqrt{{i}}−{i}\right)}{\mathrm{1}+{i}}.\frac{\mathrm{1}−{i}}{\mathrm{1}−{i}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{i}+\mathrm{2}{i}\sqrt{{i}}+\mathrm{2}\sqrt{{i}}−{i}−\mathrm{1}\right)={i}\sqrt{{i}}+\sqrt{{i}}−{i} \\ $$$$\frac{\mathrm{1}+{a}}{\mathrm{1}−{a}}=\frac{\left(\mathrm{1}+{a}\right)^{\mathrm{2}} }{\mathrm{1}−{a}^{\mathrm{2}} }=\frac{\mathrm{1}+\mathrm{2}\sqrt{{i}}+{i}}{\mathrm{1}−{i}}.\frac{\mathrm{1}+{i}}{\mathrm{1}+{i}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{i}+\mathrm{2}\sqrt{{i}}+\mathrm{2}{i}\sqrt{{i}}+{i}−\mathrm{1}\right)={i}\sqrt{{i}}+\sqrt{{i}}+{i} \\ $$
Commented by math khazana by abdo last updated on 18/Jun/18
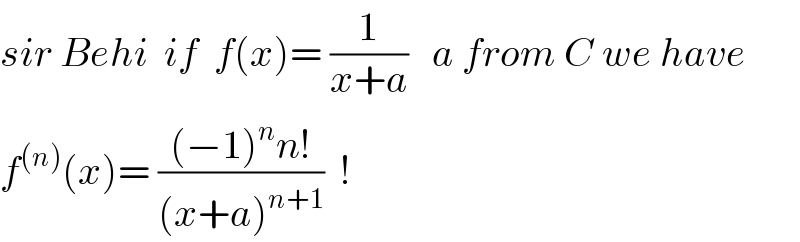
sir Behi if f(x)= (1/(x+a)) a from C we have f^((n)) (x)= (((−1)^n n!)/((x+a)^(n+1) )) !
$${sir}\:{Behi}\:\:{if}\:\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{{x}+{a}}\:\:\:{a}\:{from}\:{C}\:{we}\:{have} \\ $$$${f}^{\left({n}\right)} \left({x}\right)=\:\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({x}+{a}\right)^{{n}+\mathrm{1}} }\:\:! \\ $$
Commented by behi83417@gmail.com last updated on 18/Jun/18
corrected! thanks.
$${corrected}!\:{thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *