Menu Close

Question-168894

Tinku Tara 0 Comments
Pin




Question Number 168894 by mnjuly1970 last updated on 20/Apr/22
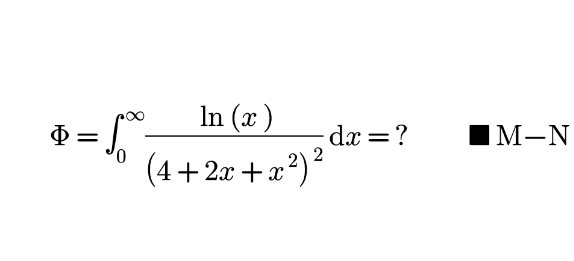
Commented by mahdipoor last updated on 20/Apr/22
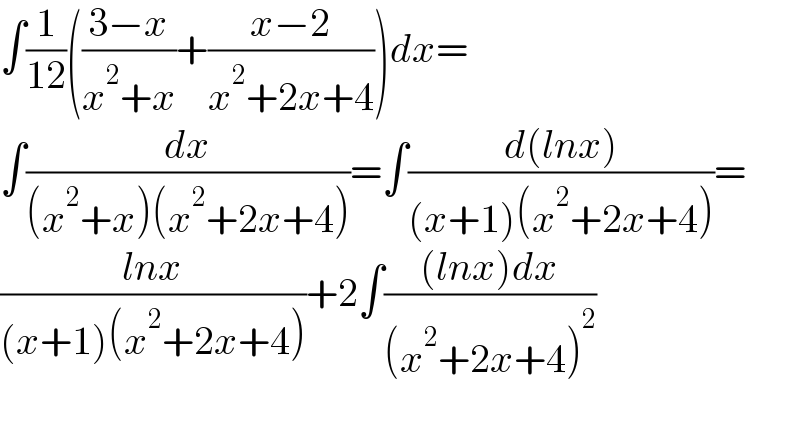
∫(1/(12))(((3−x)/(x^2 +x))+((x−2)/(x^2 +2x+4)))dx= ∫(dx/((x^2 +x)(x^2 +2x+4)))=∫((d(lnx))/((x+1)(x^2 +2x+4)))= ((lnx)/((x+1)(x^2 +2x+4)))+2∫(((lnx)dx)/((x^2 +2x+4)^2 ))
$$\int\frac{\mathrm{1}}{\mathrm{12}}\left(\frac{\mathrm{3}−{x}}{{x}^{\mathrm{2}} +{x}}+\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}}\right){dx}= \\ $$$$\int\frac{{dx}}{\left({x}^{\mathrm{2}} +{x}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)}=\int\frac{{d}\left({lnx}\right)}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)}= \\ $$$$\frac{{lnx}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)}+\mathrm{2}\int\frac{\left({lnx}\right){dx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)^{\mathrm{2}} } \\ $$$$ \\ $$
Answered by Mathspace last updated on 21/Apr/22
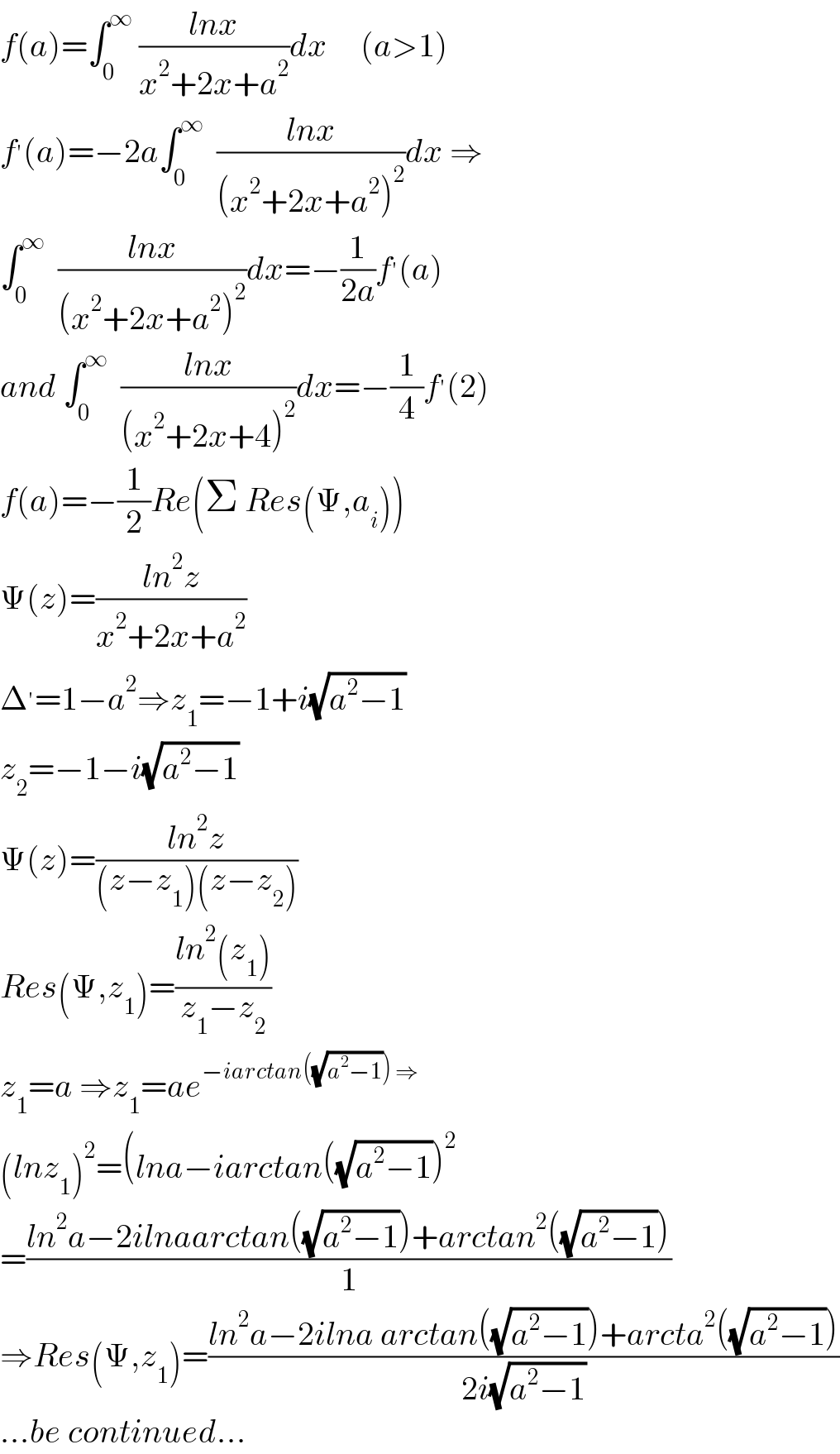
f(a)=∫_0 ^∞ ((lnx)/(x^2 +2x+a^2 ))dx (a>1) f^′ (a)=−2a∫_0 ^∞ ((lnx)/((x^2 +2x+a^2 )^2 ))dx ⇒ ∫_0 ^∞ ((lnx)/((x^2 +2x+a^2 )^2 ))dx=−(1/(2a))f^′ (a) and ∫_0 ^∞ ((lnx)/((x^2 +2x+4)^2 ))dx=−(1/4)f^′ (2) f(a)=−(1/2)Re(Σ Res(Ψ,a_i )) Ψ(z)=((ln^2 z)/(x^2 +2x+a^2 )) Δ^′ =1−a^2 ⇒z_1 =−1+i(√(a^2 −1)) z_2 =−1−i(√(a^2 −1)) Ψ(z)=((ln^2 z)/((z−z_1 )(z−z_2 ))) Res(Ψ,z_1 )=((ln^2 (z_1 ))/(z_1 −z_2 )) z_1 =a ⇒z_1 =ae^(−iarctan((√(a^2 −1))) ⇒) (lnz_1 )^2 =(lna−iarctan((√(a^2 −1)))^2 =((ln^2 a−2ilnaarctan((√(a^2 −1)))+arctan^2 ((√(a^2 −1))))/1) ⇒Res(Ψ,z_1 )=((ln^2 a−2ilna arctan((√(a^2 −1)))+arcta^2 ((√(a^2 −1))))/(2i(√(a^2 −1)))) ...be continued...
$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+{a}^{\mathrm{2}} }{dx}\:\:\:\:\:\left({a}>\mathrm{1}\right) \\ $$$${f}^{'} \left({a}\right)=−\mathrm{2}{a}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=−\frac{\mathrm{1}}{\mathrm{2}{a}}{f}^{'} \left({a}\right) \\ $$$${and}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnx}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{4}\right)^{\mathrm{2}} }{dx}=−\frac{\mathrm{1}}{\mathrm{4}}{f}^{'} \left(\mathrm{2}\right) \\ $$$${f}\left({a}\right)=−\frac{\mathrm{1}}{\mathrm{2}}{Re}\left(\Sigma\:{Res}\left(\Psi,{a}_{{i}} \right)\right) \\ $$$$\Psi\left({z}\right)=\frac{{ln}^{\mathrm{2}} {z}}{{x}^{\mathrm{2}} +\mathrm{2}{x}+{a}^{\mathrm{2}} } \\ $$$$\Delta^{'} =\mathrm{1}−{a}^{\mathrm{2}} \Rightarrow{z}_{\mathrm{1}} =−\mathrm{1}+{i}\sqrt{{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$${z}_{\mathrm{2}} =−\mathrm{1}−{i}\sqrt{{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Psi\left({z}\right)=\frac{{ln}^{\mathrm{2}} {z}}{\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)} \\ $$$${Res}\left(\Psi,{z}_{\mathrm{1}} \right)=\frac{{ln}^{\mathrm{2}} \left({z}_{\mathrm{1}} \right)}{{z}_{\mathrm{1}} −{z}_{\mathrm{2}} } \\ $$$${z}_{\mathrm{1}} ={a}\:\Rightarrow{z}_{\mathrm{1}} ={ae}^{−{iarctan}\left(\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)\:\Rightarrow} \\ $$$$\left({lnz}_{\mathrm{1}} \right)^{\mathrm{2}} =\left({lna}−{iarctan}\left(\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)^{\mathrm{2}} \right. \\ $$$$=\frac{{ln}^{\mathrm{2}} {a}−\mathrm{2}{ilnaarctan}\left(\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)+{arctan}^{\mathrm{2}} \left(\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)}{\mathrm{1}} \\ $$$$\Rightarrow{Res}\left(\Psi,{z}_{\mathrm{1}} \right)=\frac{{ln}^{\mathrm{2}} {a}−\mathrm{2}{ilna}\:{arctan}\left(\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)+{arcta}^{\mathrm{2}} \left(\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}\right)}{\mathrm{2}{i}\sqrt{{a}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$…{be}\:{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *