Menu Close

ind-the-value-of-f-a-0-dx-x-2-a-2-x-2-dx-witha-gt-0-2-calculate-f-a-

Tinku Tara 0 Comments
Pin




Question Number 37902 by math khazana by abdo last updated on 19/Jun/18
ind the value of f(a) =∫_0 ^(+∞) (dx/(x^2 +(√(a^2 +x^2 )))) dx witha>0 2)calculate f^′ (a) .
$${ind}\:{the}\:{value}\:{of}\:{f}\left({a}\right)\:\:=\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \:+\sqrt{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }}\:{dx} \\ $$$${witha}>\mathrm{0} \\ $$$$\left.\mathrm{2}\right){calculate}\:{f}^{'} \left({a}\right)\:. \\ $$
Commented by prof Abdo imad last updated on 19/Jun/18
changement x=a tan t give f(a) = ∫_0 ^(π/2) (1/(a^2 tan^2 t + a cost)) a(1+tan^2 t)dt = ∫_0 ^(π/2) ((1+tan^2 t)/(a tant +cost)) dt chang. tan((t/2))=u give f(a) = ∫_0 ^1 ((1+( ((2u)/(1−u^2 )))^2 )/(a ((2u)/(1−u^2 )) +((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) = 2 ∫_0 ^1 (((1−u^2 )^2 +4u^2 )/((1+u^2 )(1−u^2 )^2 { ((2au)/(1−u^2 )) +((1−u^2 )/(1+u^2 ))}))du = 2 ∫_0 ^1 (((1−u^2 )^2 +4u^2 )/(2au(1−u^4 ) +(1−u^2 )^3 )) du =2 ∫_0 ^1 (((1+u^2 )^2 )/(2au −2au^5 −(u^(6 ) +3u^4 −3u^2 −1)))du =2∫_0 ^1 ((u^4 +2u^(2 ) +1)/(−u^6 −2au^5 +3u^2 +2au +1))du =−2 ∫_0 ^1 ((u^4 +2u^2 +1)/(u^6 +2au^5 −3u^2 −2au −1))du...be continued...
$${changement}\:{x}={a}\:{tan}\:{t}\:{give} \\ $$$${f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\:\frac{\mathrm{1}}{{a}^{\mathrm{2}} {tan}^{\mathrm{2}} {t}\:\:+\:{a}\:{cost}}\:{a}\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} {t}}{{a}\:{tant}\:+{cost}}\:{dt}\:\:{chang}.\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u} \\ $$$${give} \\ $$$${f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{\mathrm{1}+\left(\:\frac{\mathrm{2}{u}}{\mathrm{1}−{u}^{\mathrm{2}} }\right)^{\mathrm{2}} }{{a}\:\frac{\mathrm{2}{u}}{\mathrm{1}−{u}^{\mathrm{2}} }\:\:+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\:\:\frac{\left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{4}{u}^{\mathrm{2}} }{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\mathrm{2}} \left\{\:\frac{\mathrm{2}{au}}{\mathrm{1}−{u}^{\mathrm{2}} }\:+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }\right\}}{du} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{\left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{4}{u}^{\mathrm{2}} }{\mathrm{2}{au}\left(\mathrm{1}−{u}^{\mathrm{4}} \right)\:+\left(\mathrm{1}−{u}^{\mathrm{2}} \right)^{\mathrm{3}} }\:{du} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}{au}\:−\mathrm{2}{au}^{\mathrm{5}} \:\:−\left({u}^{\mathrm{6}\:} \:+\mathrm{3}{u}^{\mathrm{4}} \:−\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}\right)}{du} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\:\frac{{u}^{\mathrm{4}} \:+\mathrm{2}{u}^{\mathrm{2}\:} \:+\mathrm{1}}{−{u}^{\mathrm{6}} \:−\mathrm{2}{au}^{\mathrm{5}} \:+\mathrm{3}{u}^{\mathrm{2}} \:+\mathrm{2}{au}\:+\mathrm{1}}{du} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\:\frac{{u}^{\mathrm{4}} \:+\mathrm{2}{u}^{\mathrm{2}} \:+\mathrm{1}}{{u}^{\mathrm{6}} \:+\mathrm{2}{au}^{\mathrm{5}} \:−\mathrm{3}{u}^{\mathrm{2}} \:−\mathrm{2}{au}\:−\mathrm{1}}{du}…{be} \\ $$$${continued}… \\ $$
Answered by ajfour last updated on 19/Jun/18
let x=atan θ f(a)=∫_0 ^( π/2) ((sec^2 θdθ)/(atan^2 θ+sec θ)) =∫_0 ^( π/2) (dθ/(asin^2 θ+cos θ)) let tan (θ/2)=t =∫_0 ^( 1) (((2dt)/(1+t^2 ))/(a(((2t)/(1+t^2 )))^2 +((1−t^2 )/(1+t^2 )))) = ∫_0 ^( 1) ((2(1+t^2 )dt)/(4at^2 +1−t^4 )) let t^4 −4at^2 +1=0 ⇒ t^2 =((4a±(√(16a^2 −4)))/2) say α, β = 2a±(√(4a^2 −1)) f(a)=−∫_0 ^( 1) ((1+t^2 )/((t^2 −α)(t^2 −β)))dt =−((α+1)/(α−β))∫_0 ^( 1) (dt/(t^2 −α))+((1+β)/(α−β))∫_0 ^( 1) (dt/(t^2 −β)) =−((α+1)/(α−β))×(1/(2(√α)))ln ∣((t−(√α))/(t+(√α)))∣_0 ^1 +((1+β)/(α−β))×(1/(2(√β)))ln ∣((t−(√β))/(t+(√β)))∣_0 ^1 not satisfactory, i guess !
$${let}\:{x}={a}\mathrm{tan}\:\theta \\ $$$$\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \frac{\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta}{{a}\mathrm{tan}\:^{\mathrm{2}} \theta+\mathrm{sec}\:\theta} \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\:\:\pi/\mathrm{2}} \frac{{d}\theta}{{a}\mathrm{sin}\:^{\mathrm{2}} \theta+\mathrm{cos}\:\theta} \\ $$$$\:\:\:\:{let}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}={t} \\ $$$$\:\:\:\:\:=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }}{{a}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\right)^{\mathrm{2}} +\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$$\:\:\:\:=\:\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dt}}{\mathrm{4}{at}^{\mathrm{2}} +\mathrm{1}−{t}^{\mathrm{4}} } \\ $$$${let}\:\:\:{t}^{\mathrm{4}} −\mathrm{4}{at}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:{t}^{\mathrm{2}} =\frac{\mathrm{4}{a}\pm\sqrt{\mathrm{16}{a}^{\mathrm{2}} −\mathrm{4}}}{\mathrm{2}}\: \\ $$$$\:\:\:{say}\:\:\:\alpha,\:\beta\:\:=\:\mathrm{2}{a}\pm\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$${f}\left({a}\right)=−\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{\mathrm{1}+{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\alpha\right)\left({t}^{\mathrm{2}} −\beta\right)}{dt} \\ $$$$\:\:\:=−\frac{\alpha+\mathrm{1}}{\alpha−\beta}\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{2}} −\alpha}+\frac{\mathrm{1}+\beta}{\alpha−\beta}\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{{dt}}{{t}^{\mathrm{2}} −\beta} \\ $$$$\:\:=−\frac{\alpha+\mathrm{1}}{\alpha−\beta}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\alpha}}\mathrm{ln}\:\mid\frac{{t}−\sqrt{\alpha}}{{t}+\sqrt{\alpha}}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}+\beta}{\alpha−\beta}×\frac{\mathrm{1}}{\mathrm{2}\sqrt{\beta}}\mathrm{ln}\:\mid\frac{{t}−\sqrt{\beta}}{{t}+\sqrt{\beta}}\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:\:{not}\:{satisfactory},\:{i}\:{guess}\:! \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jun/18
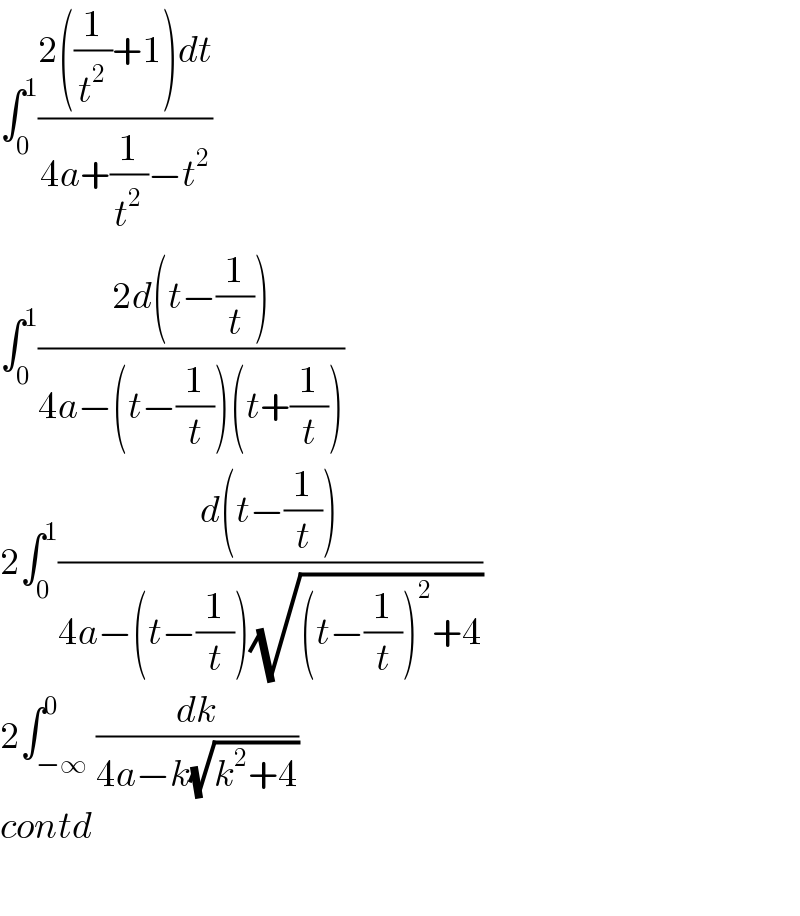
∫_0 ^1 ((2((1/t^2 )+1)dt)/(4a+(1/t^2 )−t^2 )) ∫_0 ^1 ((2d(t−(1/t)))/(4a−(t−(1/t))(t+(1/t)))) 2∫_0 ^1 ((d(t−(1/t)))/(4a−(t−(1/t))(√((t−(1/t))^2 +4)))) 2∫_(−∞) ^0 (dk/(4a−k(√(k^2 +4)))) contd
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\mathrm{1}\right){dt}}{\mathrm{4}{a}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} }−{t}^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{d}\left({t}−\frac{\mathrm{1}}{{t}}\right)}{\mathrm{4}{a}−\left({t}−\frac{\mathrm{1}}{{t}}\right)\left({t}+\frac{\mathrm{1}}{{t}}\right)} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{d}\left({t}−\frac{\mathrm{1}}{{t}}\right)}{\mathrm{4}{a}−\left({t}−\frac{\mathrm{1}}{{t}}\right)\sqrt{\left({t}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\mathrm{4}}} \\ $$$$\mathrm{2}\int_{−\infty} ^{\mathrm{0}} \frac{{dk}}{\mathrm{4}{a}−{k}\sqrt{{k}^{\mathrm{2}} +\mathrm{4}}} \\ $$$${contd} \\ $$$$ \\ $$
Answered by MJS last updated on 19/Jun/18
this is the method: ∫(dx/(x^2 +(√(x^2 +a^2 ))))=∫(x^2 /(x^4 −x^2 −a^2 ))dx−∫((√(x^2 +a^2 ))/(x^4 −x^2 −a^2 ))dx ∫(x^2 /(x^4 −x^2 −a^2 ))dx= =Σ_(i=1) ^4 ∫(N_i /(x−r_i ))dx=Σ_(i=1) ^4 N_i ln∣x−r_i ∣ ∫((√(x^2 +a^2 ))/(x^4 −x^2 −a^2 ))dx= [t=(x/( (√(x^2 +a^2 )))) → dx=(dt/a^2 )(√((x^2 +a^2 )^3 ))] =(1/a^2 )∫(dt/(t^4 +(1/a^2 )t^2 −(1/a^2 )))= =(N_5 /a^2 )(∫(dt/(t−r_5 ))−∫(dt/(t+r_5 )))+(N_6 /a^2 )∫(dt/(t^2 +r_6 ))= [r_6 >0] =(N_5 /a^2 )ln∣((t−r_5 )/(t+r_5 ))∣+(N_6 /(a^2 (√r_6 )))arctan (t/( (√r_6 )))= =(N_5 /a^2 )ln∣(((x/( (√(x^2 +a^2 ))))−r_5 )/((x/( (√(x^2 +a^2 ))))+r_5 ))∣+(N_6 /(a^2 (√r_6 )))arctan (x/( (√(r_6 (x^2 +a^2 )))))
$$\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{method}: \\ $$$$ \\ $$$$\int\frac{{dx}}{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}=\int\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx}−\int\frac{\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\int\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:=\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}\int\frac{\mathcal{N}_{{i}} }{{x}−{r}_{{i}} }{dx}=\underset{{i}=\mathrm{1}} {\overset{\mathrm{4}} {\sum}}\mathcal{N}_{{i}} \mathrm{ln}\mid{x}−{r}_{{i}} \mid \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}\:\rightarrow\:{dx}=\frac{{dt}}{{a}^{\mathrm{2}} }\sqrt{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{3}} }\right] \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{{a}^{\mathrm{2}} }\int\frac{{dt}}{{t}^{\mathrm{4}} +\frac{\mathrm{1}}{{a}^{\mathrm{2}} }{t}^{\mathrm{2}} −\frac{\mathrm{1}}{{a}^{\mathrm{2}} }}= \\ $$$$\:\:\:\:\:=\frac{\mathcal{N}_{\mathrm{5}} }{{a}^{\mathrm{2}} }\left(\int\frac{{dt}}{{t}−{r}_{\mathrm{5}} }−\int\frac{{dt}}{{t}+{r}_{\mathrm{5}} }\right)+\frac{\mathcal{N}_{\mathrm{6}} }{{a}^{\mathrm{2}} }\int\frac{{dt}}{{t}^{\mathrm{2}} +{r}_{\mathrm{6}} }= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{r}_{\mathrm{6}} >\mathrm{0}\right] \\ $$$$\:\:\:\:\:=\frac{\mathcal{N}_{\mathrm{5}} }{{a}^{\mathrm{2}} }\mathrm{ln}\mid\frac{{t}−{r}_{\mathrm{5}} }{{t}+{r}_{\mathrm{5}} }\mid+\frac{\mathcal{N}_{\mathrm{6}} }{{a}^{\mathrm{2}} \sqrt{{r}_{\mathrm{6}} }}\mathrm{arctan}\:\frac{{t}}{\:\sqrt{{r}_{\mathrm{6}} }}= \\ $$$$\:\:\:\:\:=\frac{\mathcal{N}_{\mathrm{5}} }{{a}^{\mathrm{2}} }\mathrm{ln}\mid\frac{\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}−{r}_{\mathrm{5}} }{\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }}+{r}_{\mathrm{5}} }\mid+\frac{\mathcal{N}_{\mathrm{6}} }{{a}^{\mathrm{2}} \sqrt{{r}_{\mathrm{6}} }}\mathrm{arctan}\:\frac{{x}}{\:\sqrt{{r}_{\mathrm{6}} \left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)}} \\ $$
Commented by MJS last updated on 20/Jun/18
r_1 =−((√2)/2)(√(1−(√(4a^2 +1)))) r_2 =−((√2)/2)(√(1+(√(4a^2 +1)))) r_3 =((√2)/2)(√(1−(√(4a^2 +1)))) r_4 =((√2)/2)(√(1+(√(4a^2 +1)))) r_5 =((√2)/(2a))(√(−1+(√(4a^2 +1)))) r_6 =((1+(√(4a^2 +1)))/(2a^2 )) N_1 =((√(2−2(√(4a^2 +1))))/(4(√(4a^2 +1)))) N_2 =−((√(2+2(√(4a^2 +1))))/(4(√(4a^2 +1)))) N_3 =−((√(2−2(√(4a^2 +1))))/(4(√(4a^2 +1)))) N_4 =((√(2+2(√(4a^2 +1))))/(4(√(4a^2 +1)))) N_5 =((a^3 (√2))/(2(√((4a^2 +1)(−1+(√(4a^2 +1))))))) N_6 =−(a^2 /( (√(4a^2 +1))))
$${r}_{\mathrm{1}} =−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}−\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${r}_{\mathrm{2}} =−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${r}_{\mathrm{3}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}−\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${r}_{\mathrm{4}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\sqrt{\mathrm{1}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${r}_{\mathrm{5}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}{a}}\sqrt{−\mathrm{1}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${r}_{\mathrm{6}} =\frac{\mathrm{1}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}{a}^{\mathrm{2}} } \\ $$$$\mathcal{N}_{\mathrm{1}} =\frac{\sqrt{\mathrm{2}−\mathrm{2}\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}}}{\mathrm{4}\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathcal{N}_{\mathrm{2}} =−\frac{\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}}}{\mathrm{4}\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathcal{N}_{\mathrm{3}} =−\frac{\sqrt{\mathrm{2}−\mathrm{2}\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}}}{\mathrm{4}\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathcal{N}_{\mathrm{4}} =\frac{\sqrt{\mathrm{2}+\mathrm{2}\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}}}{\mathrm{4}\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathcal{N}_{\mathrm{5}} =\frac{{a}^{\mathrm{3}} \sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\left(\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}\right)\left(−\mathrm{1}+\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}\right)}} \\ $$$$\mathcal{N}_{\mathrm{6}} =−\frac{{a}^{\mathrm{2}} }{\:\sqrt{\mathrm{4}{a}^{\mathrm{2}} +\mathrm{1}}} \\ $$
Commented by math khazana by abdo last updated on 20/Jun/18
thank you sir Mjs
$${thank}\:{you}\:{sir}\:{Mjs} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *