Question Number 169049 by Mastermind last updated on 23/Apr/22

$$\int{x}^{\mathrm{2}} {e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by Mathspace last updated on 23/Apr/22
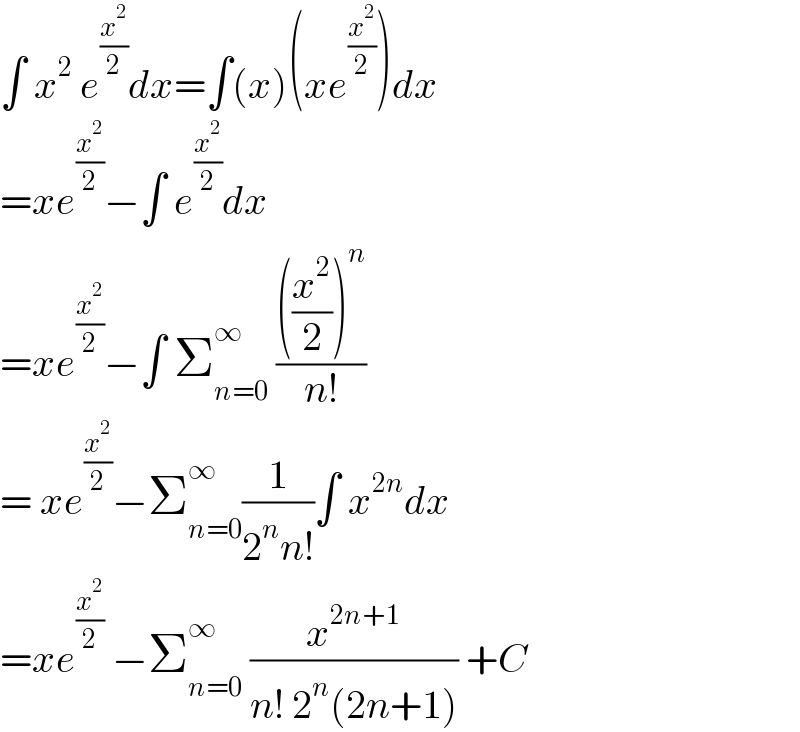
$$\int\:{x}^{\mathrm{2}} \:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {dx}=\int\left({x}\right)\left({xe}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \right){dx} \\ $$$$={xe}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} −\int\:{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {dx} \\ $$$$={xe}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} −\int\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)^{{n}} }{{n}!} \\ $$$$=\:{xe}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} −\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}!}\int\:{x}^{\mathrm{2}{n}} {dx} \\ $$$$={xe}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{{n}!\:\mathrm{2}^{{n}} \left(\mathrm{2}{n}+\mathrm{1}\right)}\:+{C} \\ $$
