Question-169078

Question Number 169078 by MikeH last updated on 23/Apr/22

Answered by mahdipoor last updated on 23/Apr/22

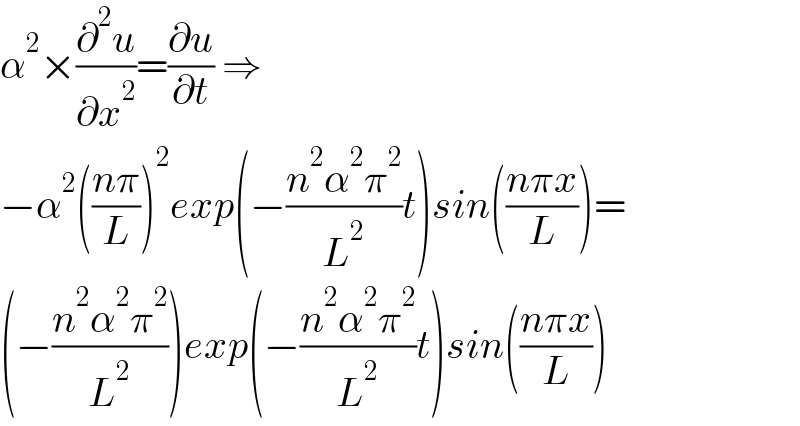
α^2 ×(∂^2 u/∂x^2 )=(∂u/∂t) ⇒ −α^2 (((nπ)/L))^2 exp(−((n^2 α^2 π^2 )/L^2 )t)sin(((nπx)/L))= (−((n^2 α^2 π^2 )/L^2 ))exp(−((n^2 α^2 π^2 )/L^2 )t)sin(((nπx)/L))

$$\alpha^{\mathrm{2}} ×\frac{\partial^{\mathrm{2}} {u}}{\partial{x}^{\mathrm{2}} }=\frac{\partial{u}}{\partial{t}}\:\Rightarrow \\ $$$$−\alpha^{\mathrm{2}} \left(\frac{{n}\pi}{{L}}\right)^{\mathrm{2}} {exp}\left(−\frac{{n}^{\mathrm{2}} \alpha^{\mathrm{2}} \pi^{\mathrm{2}} }{{L}^{\mathrm{2}} }{t}\right){sin}\left(\frac{{n}\pi{x}}{{L}}\right)= \\ $$$$\left(−\frac{{n}^{\mathrm{2}} \alpha^{\mathrm{2}} \pi^{\mathrm{2}} }{{L}^{\mathrm{2}} }\right){exp}\left(−\frac{{n}^{\mathrm{2}} \alpha^{\mathrm{2}} \pi^{\mathrm{2}} }{{L}^{\mathrm{2}} }{t}\right){sin}\left(\frac{{n}\pi{x}}{{L}}\right) \\ $$

Commented by MikeH last updated on 24/Apr/22

$$\mathrm{perfect} \\ $$

Facebook Tweet Pin

Question-169078

Leave a Reply Cancel reply