Question Number 38190 by ajfour last updated on 22/Jun/18

Commented by ajfour last updated on 22/Jun/18

$$\:\:\:\:\:\:\:\boldsymbol{{What}}\:\boldsymbol{{is}}\:\boldsymbol{{the}}\:\boldsymbol{{time}}\:\boldsymbol{{in}}\:\boldsymbol{{the}}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{outer}}\:\boldsymbol{{clock}}\:? \\ $$$$\:\:{Ignore}\:{the}\:{minute}\:{hand}\:{of}\:{the} \\ $$$${bigger}\:{clock}.\:{Then}\:{it}\:{will}\:{be}\:{a} \\ $$$${correct}\:{question},\:{i}\:{think}\:{now}. \\ $$
Commented by MrW3 last updated on 23/Jun/18
![let θ=tan^(−1) 2≈63.43° ((sin α)/( (√5)a))=((sin ((π/2)+(π/2)−θ))/(8a)) ⇒sin α=((√5)/8) sin θ=((√5)/8)×(2/( (√5)))=(1/4) ⇒α=sin^(−1) (1/4)≈14.48° ⇒((5×14.48)/(30))=2.41min≡2min24sec ((sin β)/( (√5)a))=((sin (θ+(π/6)))/(8a)) ⇒sin β=((√5)/8) sin (θ+(π/6))=((√5)/8)((2/( (√5)))×((√3)/2)+(1/( (√5)))×(1/2))=((2(√3)+1)/(16)) ⇒β=sin^(−1) [((2(√3)+1)/(16))]≈16.2° γ=180°−β−30°=133.8° ⇒((133.8)/(30))=4.46H≡4H27M36S](https://www.tinkutara.com/question/Q38196.png)
$${let}\:\theta=\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\approx\mathrm{63}.\mathrm{43}° \\ $$$$\frac{\mathrm{sin}\:\alpha}{\:\sqrt{\mathrm{5}}{a}}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}+\frac{\pi}{\mathrm{2}}−\theta\right)}{\mathrm{8}{a}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{5}}}{\mathrm{8}}\:\mathrm{sin}\:\theta=\frac{\sqrt{\mathrm{5}}}{\mathrm{8}}×\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\alpha=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{4}}\approx\mathrm{14}.\mathrm{48}° \\ $$$$\Rightarrow\frac{\mathrm{5}×\mathrm{14}.\mathrm{48}}{\mathrm{30}}=\mathrm{2}.\mathrm{41}{min}\equiv\mathrm{2}{min}\mathrm{24}{sec} \\ $$$$ \\ $$$$\frac{\mathrm{sin}\:\beta}{\:\sqrt{\mathrm{5}}{a}}=\frac{\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)}{\mathrm{8}{a}} \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{\sqrt{\mathrm{5}}}{\mathrm{8}}\:\mathrm{sin}\:\left(\theta+\frac{\pi}{\mathrm{6}}\right)=\frac{\sqrt{\mathrm{5}}}{\mathrm{8}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}×\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{16}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \left[\frac{\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{16}}\right]\approx\mathrm{16}.\mathrm{2}° \\ $$$$\gamma=\mathrm{180}°−\beta−\mathrm{30}°=\mathrm{133}.\mathrm{8}° \\ $$$$\Rightarrow\frac{\mathrm{133}.\mathrm{8}}{\mathrm{30}}=\mathrm{4}.\mathrm{46}{H}\equiv\mathrm{4}{H}\mathrm{27}{M}\mathrm{36}{S} \\ $$
Answered by ajfour last updated on 23/Jun/18
![Ignoring the minute hand, the time in outer clock by its hour hand : let ∠ of hour hand of bigger clock from postion 6 o′clck be θ. 8asin θ=2a+(8acos θ+a)tan 30° 8(sin θ−((cos θ)/( (√3))))=2+(1/( (√3))) 8((√3)sin θ−cos θ)=1+2(√3) sin (θ−(π/6))=((1+2(√3))/(16)) θ=(π/6)+sin^(−1) (((1+2(√3))/(16))) H=6−(6/π)[(π/6)+sin^(−1) (((1+2(√3))/(16)))] H = 5−(6/π)sin^(−1) (((1+2(√3))/(16))) . __(wrong previous answer) t =[ 4+(6/𝛑)sin^(−1) (((1+2(√3))/(16))) ] hours .](https://www.tinkutara.com/question/Q38192.png)
$${Ignoring}\:{the}\:{minute}\:{hand}, \\ $$$${the}\:{time}\:{in}\:{outer}\:{clock}\:{by}\:{its} \\ $$$${hour}\:{hand}\:: \\ $$$${let}\:\angle\:{of}\:{hour}\:{hand}\:{of}\:{bigger}\:{clock} \\ $$$${from}\:{postion}\:\mathrm{6}\:{o}'{clck}\:{be}\:\theta. \\ $$$$\mathrm{8}{a}\mathrm{sin}\:\theta=\mathrm{2}{a}+\left(\mathrm{8}{a}\mathrm{cos}\:\theta+{a}\right)\mathrm{tan}\:\mathrm{30}° \\ $$$$\mathrm{8}\left(\mathrm{sin}\:\theta−\frac{\mathrm{cos}\:\theta}{\:\sqrt{\mathrm{3}}}\right)=\mathrm{2}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{8}\left(\sqrt{\mathrm{3}}\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)=\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\mathrm{sin}\:\left(\theta−\frac{\pi}{\mathrm{6}}\right)=\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{16}} \\ $$$$\theta=\frac{\pi}{\mathrm{6}}+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{16}}\right) \\ $$$${H}=\mathrm{6}−\frac{\mathrm{6}}{\pi}\left[\frac{\pi}{\mathrm{6}}+\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{16}}\right)\right] \\ $$$$\:\:{H}\:=\:\mathrm{5}−\frac{\mathrm{6}}{\pi}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{16}}\right)\:. \\ $$$$\underset{{wrong}\:{previous}\:{answer}} {\_} \\ $$$$\:\boldsymbol{{t}}\:=\left[\:\mathrm{4}+\frac{\mathrm{6}}{\boldsymbol{\pi}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{16}}\right)\:\right]\:{hours}\:. \\ $$
Commented by MrW3 last updated on 23/Jun/18
![please check sir. should it not be t =[5−(6/𝛑)sin^(−1) (((1+2(√3))/(16))) ] hours ?](https://www.tinkutara.com/question/Q38231.png)
$${please}\:{check}\:{sir}.\:{should}\:{it}\:{not}\:{be} \\ $$$$\:\boldsymbol{{t}}\:=\left[\mathrm{5}−\frac{\mathrm{6}}{\boldsymbol{\pi}}\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{16}}\right)\:\right]\:{hours}\:? \\ $$
Commented by ajfour last updated on 23/Jun/18
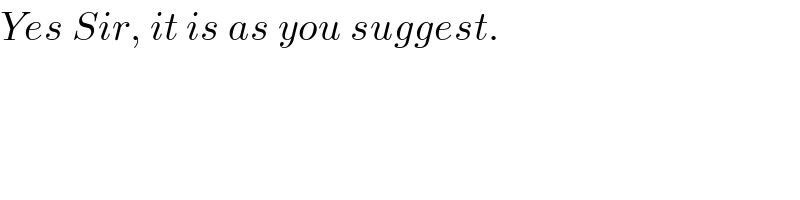
$${Yes}\:{Sir},\:{it}\:{is}\:{as}\:{you}\:{suggest}. \\ $$
