Question Number 169273 by cortano1 last updated on 27/Apr/22
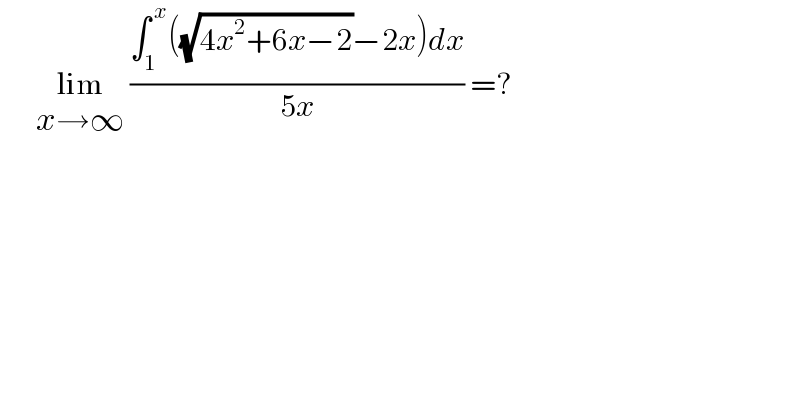
$$\:\:\:\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\int_{\mathrm{1}} ^{\:{x}} \left(\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{2}}−\mathrm{2}{x}\right){dx}}{\mathrm{5}{x}}\:=? \\ $$
Answered by qaz last updated on 28/Apr/22
![lim_(x→+∞) ((∫_1 ^x (√(4t^2 +6t−2))−2tdt)/(5x)) =lim_(x→+∞) ((O(1)+∫_2 ^x (√(4t^2 +6t−2))−2tdt)/(5x)) =lim_(x→+∞) ((O(1)+∫_2 ^x [(2t+(3/2)+O((1/t)))−2t]dt)/(5x)) =lim_(x→+∞) ((O(1)+(3/2)x+O(lnx))/(5x)) =(3/(10))](https://www.tinkutara.com/question/Q169290.png)
$$\underset{\mathrm{x}\rightarrow+\infty} {\mathrm{lim}}\frac{\int_{\mathrm{1}} ^{\mathrm{x}} \sqrt{\mathrm{4t}^{\mathrm{2}} +\mathrm{6t}−\mathrm{2}}−\mathrm{2tdt}}{\mathrm{5x}} \\ $$$$=\underset{\mathrm{x}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathcal{O}\left(\mathrm{1}\right)+\int_{\mathrm{2}} ^{\mathrm{x}} \sqrt{\mathrm{4t}^{\mathrm{2}} +\mathrm{6t}−\mathrm{2}}−\mathrm{2tdt}}{\mathrm{5x}} \\ $$$$=\underset{\mathrm{x}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathcal{O}\left(\mathrm{1}\right)+\int_{\mathrm{2}} ^{\mathrm{x}} \left[\left(\mathrm{2t}+\frac{\mathrm{3}}{\mathrm{2}}+\mathcal{O}\left(\frac{\mathrm{1}}{\mathrm{t}}\right)\right)−\mathrm{2t}\right]\mathrm{dt}}{\mathrm{5x}} \\ $$$$=\underset{\mathrm{x}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathcal{O}\left(\mathrm{1}\right)+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}+\mathcal{O}\left(\mathrm{lnx}\right)}{\mathrm{5x}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{10}} \\ $$
Answered by bobhans last updated on 28/Apr/22
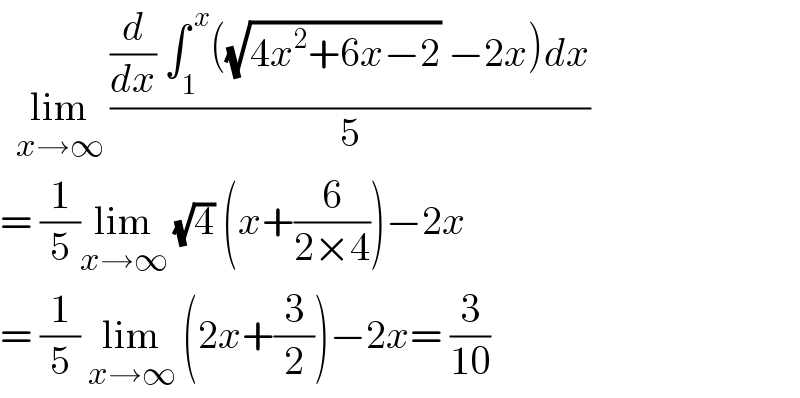
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\frac{{d}}{{dx}}\:\int_{\mathrm{1}} ^{\:{x}} \left(\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}−\mathrm{2}}\:−\mathrm{2}{x}\right){dx}}{\mathrm{5}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\sqrt{\mathrm{4}}\:\left({x}+\frac{\mathrm{6}}{\mathrm{2}×\mathrm{4}}\right)−\mathrm{2}{x} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{2}{x}+\frac{\mathrm{3}}{\mathrm{2}}\right)−\mathrm{2}{x}=\:\frac{\mathrm{3}}{\mathrm{10}} \\ $$
