Question Number 103874 by aurpeyz last updated on 17/Jul/20

Commented by aurpeyz last updated on 18/Jul/20

$$\mathrm{pls}\:\mathrm{help} \\ $$
Answered by Rio Michael last updated on 18/Jul/20
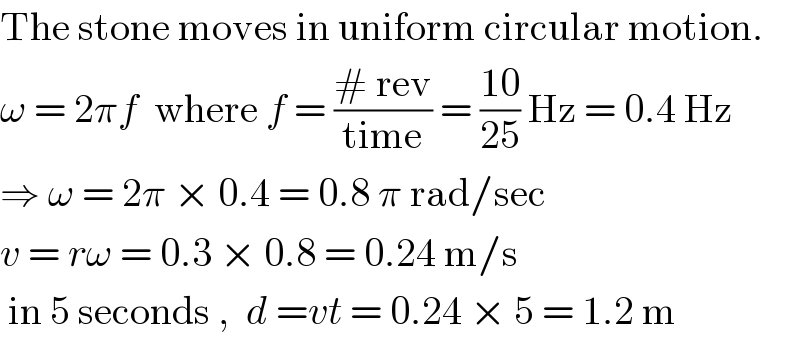
$$\mathrm{The}\:\mathrm{stone}\:\mathrm{moves}\:\mathrm{in}\:\mathrm{uniform}\:\mathrm{circular}\:\mathrm{motion}. \\ $$$$\omega\:=\:\mathrm{2}\pi{f}\:\:\mathrm{where}\:{f}\:=\:\frac{#\:\mathrm{rev}}{\mathrm{time}}\:=\:\frac{\mathrm{10}}{\mathrm{25}}\:\mathrm{Hz}\:=\:\mathrm{0}.\mathrm{4}\:\mathrm{Hz} \\ $$$$\Rightarrow\:\omega\:=\:\mathrm{2}\pi\:×\:\mathrm{0}.\mathrm{4}\:=\:\mathrm{0}.\mathrm{8}\:\pi\:\mathrm{rad}/\mathrm{sec} \\ $$$${v}\:=\:{r}\omega\:=\:\mathrm{0}.\mathrm{3}\:×\:\mathrm{0}.\mathrm{8}\:=\:\mathrm{0}.\mathrm{24}\:\mathrm{m}/\mathrm{s} \\ $$$$\:\mathrm{in}\:\mathrm{5}\:\mathrm{seconds}\:,\:\:{d}\:={vt}\:=\:\mathrm{0}.\mathrm{24}\:×\:\mathrm{5}\:=\:\mathrm{1}.\mathrm{2}\:\mathrm{m} \\ $$
Commented by aurpeyz last updated on 18/Jul/20

$$\mathrm{is}\:\mathrm{this}\:\mathrm{solution}\:\mathrm{correct}.\:\mathrm{can}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{be}\:\mathrm{the}\:\mathrm{length}\:\mathrm{of}\:\mathrm{the}\:\mathrm{rope}? \\ $$
Commented by aurpeyz last updated on 18/Jul/20

