Menu Close

a-100-cm-long-rod-should-be-divided-into-3-parts-the-length-of-each-part-in-cm-should-be-integer-in-how-many-different-ways-can-this-be-done-

Tinku Tara 0 Comments
Pin




Question Number 103903 by mr W last updated on 18/Jul/20
a 100 cm long rod should be divided into 3 parts. the length of each part in cm should be integer. in how many different ways can this be done?
$${a}\:\mathrm{100}\:{cm}\:{long}\:{rod}\:{should}\:{be}\:{divided} \\ $$$${into}\:\mathrm{3}\:{parts}.\:{the}\:{length}\:{of}\:{each}\:{part} \\ $$$${in}\:{cm}\:{should}\:{be}\:{integer}.\:{in}\:{how}\: \\ $$$${many}\:{different}\:{ways}\:{can}\:{this}\:{be} \\ $$$${done}? \\ $$
Commented by bobhans last updated on 18/Jul/20
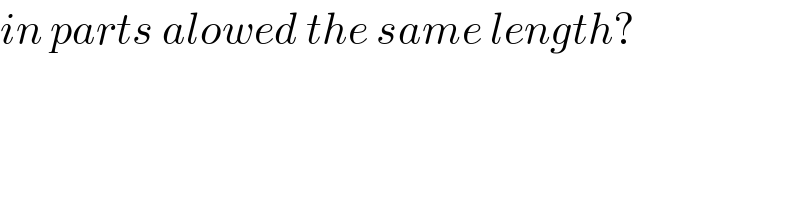
in parts alowed the same length?
$${in}\:{parts}\:{alowed}\:{the}\:{same}\:{length}? \\ $$
Commented by mr W last updated on 18/Jul/20
the only condition is: the length must be integer. so the parts may also have equal length.
$${the}\:{only}\:{condition}\:{is}:\:{the}\:{length} \\ $$$${must}\:{be}\:{integer}.\:{so}\:{the}\:{parts}\:{may} \\ $$$${also}\:{have}\:{equal}\:{length}. \\ $$
Commented by bobhans last updated on 18/Jul/20
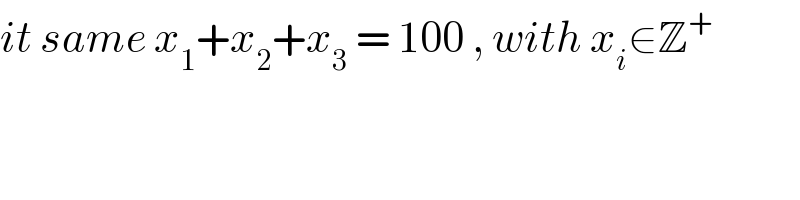
it same x_1 +x_2 +x_3 = 100 , with x_i ∈Z^+
$${it}\:{same}\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} \:=\:\mathrm{100}\:,\:{with}\:{x}_{{i}} \in\mathbb{Z}^{+} \\ $$
Commented by mr W last updated on 18/Jul/20
not exactly the same. e.g. 2+5+93 or 5+2+93 or 93+2+5 are different solutions for your equation, but they represent the one and the same way to divide the rod. the parts are not labeled.
$${not}\:{exactly}\:{the}\:{same}.\: \\ $$$${e}.{g}.\:\mathrm{2}+\mathrm{5}+\mathrm{93}\:{or}\:\mathrm{5}+\mathrm{2}+\mathrm{93}\:{or}\:\mathrm{93}+\mathrm{2}+\mathrm{5}\:{are} \\ $$$${different}\:{solutions}\:{for}\:{your} \\ $$$${equation},\:{but}\:{they}\:{represent}\:{the}\:{one} \\ $$$${and}\:{the}\:{same}\:{way}\:{to}\:{divide}\:{the}\:{rod}. \\ $$$${the}\:{parts}\:{are}\:{not}\:{labeled}. \\ $$
Commented by bobhans last updated on 18/Jul/20
o oo yes agree
$${o}\:{oo}\:{yes}\:{agree}\: \\ $$
Answered by mr W last updated on 18/Jul/20
METHOD I say the lengthes of the parts are a,b,c with a≤b≤c. a+b+c=100 100=a+b+c≥3a ⇒a≤((100)/3) ⇒a≤33 with a=1: 99=b+c≥2b ⇒b≤((99)/2) ⇒b≤49 ⇒b=1,2,...,49 ⇒49 solutions with a=2: 98=b+c≥2b ⇒b≤49 ⇒b=2,3,...,49 ⇒48 solutions with a=3: 97=b+c≥2b ⇒b≤((97)/2) ⇒b≤48 ⇒b=3,4,...,48 ⇒46 solutions with a=4: 96=b+c≥2b ⇒b≤48 ⇒b=4,5,...,48 ⇒45 solutions ..... with a=33: 67=b+c≥2b ⇒b≤((67)/2) ⇒b≤33 ⇒b=33 ⇒1 solution total number of solutions: 1+4+7+...+46+49 +3+6+9+...+45+48 =((17×(1+49))/2)+((16×(3+48))/2) =833
$$\boldsymbol{{METHOD}}\:\boldsymbol{{I}} \\ $$$${say}\:{the}\:{lengthes}\:{of}\:{the}\:{parts}\:{are} \\ $$$${a},{b},{c}\:{with}\:{a}\leqslant{b}\leqslant{c}. \\ $$$${a}+{b}+{c}=\mathrm{100} \\ $$$$\mathrm{100}={a}+{b}+{c}\geqslant\mathrm{3}{a} \\ $$$$\Rightarrow{a}\leqslant\frac{\mathrm{100}}{\mathrm{3}}\:\Rightarrow{a}\leqslant\mathrm{33} \\ $$$${with}\:{a}=\mathrm{1}: \\ $$$$\mathrm{99}={b}+{c}\geqslant\mathrm{2}{b} \\ $$$$\Rightarrow{b}\leqslant\frac{\mathrm{99}}{\mathrm{2}}\:\Rightarrow{b}\leqslant\mathrm{49} \\ $$$$\Rightarrow{b}=\mathrm{1},\mathrm{2},…,\mathrm{49}\:\Rightarrow\mathrm{49}\:{solutions} \\ $$$${with}\:{a}=\mathrm{2}: \\ $$$$\mathrm{98}={b}+{c}\geqslant\mathrm{2}{b} \\ $$$$\Rightarrow{b}\leqslant\mathrm{49} \\ $$$$\Rightarrow{b}=\mathrm{2},\mathrm{3},…,\mathrm{49}\:\Rightarrow\mathrm{48}\:{solutions} \\ $$$${with}\:{a}=\mathrm{3}: \\ $$$$\mathrm{97}={b}+{c}\geqslant\mathrm{2}{b} \\ $$$$\Rightarrow{b}\leqslant\frac{\mathrm{97}}{\mathrm{2}}\:\Rightarrow{b}\leqslant\mathrm{48} \\ $$$$\Rightarrow{b}=\mathrm{3},\mathrm{4},…,\mathrm{48}\:\Rightarrow\mathrm{46}\:{solutions} \\ $$$${with}\:{a}=\mathrm{4}: \\ $$$$\mathrm{96}={b}+{c}\geqslant\mathrm{2}{b} \\ $$$$\Rightarrow{b}\leqslant\mathrm{48} \\ $$$$\Rightarrow{b}=\mathrm{4},\mathrm{5},…,\mathrm{48}\:\Rightarrow\mathrm{45}\:{solutions} \\ $$$$….. \\ $$$${with}\:{a}=\mathrm{33}: \\ $$$$\mathrm{67}={b}+{c}\geqslant\mathrm{2}{b} \\ $$$$\Rightarrow{b}\leqslant\frac{\mathrm{67}}{\mathrm{2}}\:\Rightarrow{b}\leqslant\mathrm{33} \\ $$$$\Rightarrow{b}=\mathrm{33}\:\Rightarrow\mathrm{1}\:{solution} \\ $$$$ \\ $$$${total}\:{number}\:{of}\:{solutions}: \\ $$$$\mathrm{1}+\mathrm{4}+\mathrm{7}+…+\mathrm{46}+\mathrm{49} \\ $$$$+\mathrm{3}+\mathrm{6}+\mathrm{9}+…+\mathrm{45}+\mathrm{48} \\ $$$$=\frac{\mathrm{17}×\left(\mathrm{1}+\mathrm{49}\right)}{\mathrm{2}}+\frac{\mathrm{16}×\left(\mathrm{3}+\mathrm{48}\right)}{\mathrm{2}} \\ $$$$=\mathrm{833} \\ $$
Commented by bobhans last updated on 18/Jul/20
cooll....nice
$${cooll}….{nice} \\ $$
Commented by mr W last updated on 18/Jul/20
METHOD II say the lengthes of the parts are a,b,c with a≤b≤c. a+b+c=100 ...(i) number of solutions is the coeff. of x^(100) term of following generating function (x^3 /((1−x)(1−x^2 )(1−x^3 ))) which is 833.
$$\boldsymbol{{METHOD}}\:\boldsymbol{{II}} \\ $$$${say}\:{the}\:{lengthes}\:{of}\:{the}\:{parts}\:{are} \\ $$$${a},{b},{c}\:{with}\:{a}\leqslant{b}\leqslant{c}. \\ $$$$\boldsymbol{{a}}+\boldsymbol{{b}}+\boldsymbol{{c}}=\mathrm{100}\:\:\:…\left({i}\right) \\ $$$${number}\:{of}\:{solutions}\:{is}\:{the}\:{coeff}.\:{of} \\ $$$${x}^{\mathrm{100}} \:{term}\:{of}\:{following}\:{generating} \\ $$$${function} \\ $$$$\frac{{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{3}} \right)} \\ $$$${which}\:{is}\:\mathrm{833}. \\ $$
Commented by mr W last updated on 18/Jul/20
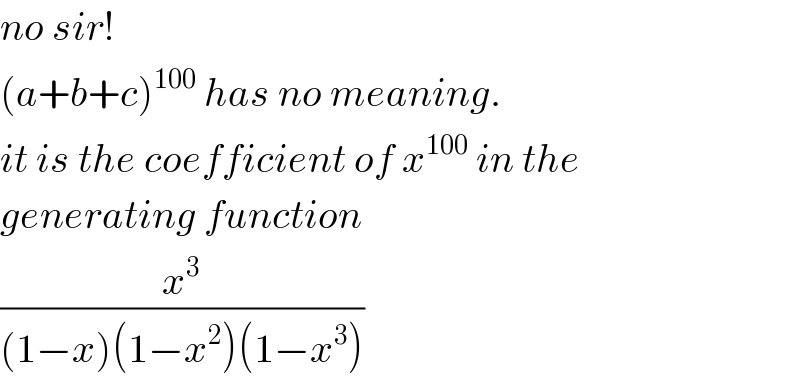
no sir! (a+b+c)^(100) has no meaning. it is the coefficient of x^(100) in the generating function (x^3 /((1−x)(1−x^2 )(1−x^3 )))
$${no}\:{sir}! \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{100}} \:{has}\:{no}\:{meaning}. \\ $$$${it}\:{is}\:{the}\:{coefficient}\:{of}\:{x}^{\mathrm{100}} \:{in}\:{the} \\ $$$${generating}\:{function} \\ $$$$\frac{{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{3}} \right)} \\ $$
Commented by mr W last updated on 18/Jul/20
Commented by bemath last updated on 18/Jul/20
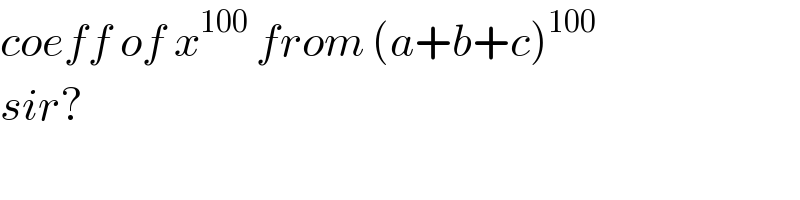
coeff of x^(100) from (a+b+c)^(100) sir?
$${coeff}\:{of}\:{x}^{\mathrm{100}} \:{from}\:\left({a}+{b}+{c}\right)^{\mathrm{100}} \\ $$$${sir}? \\ $$
Commented by mr W last updated on 18/Jul/20
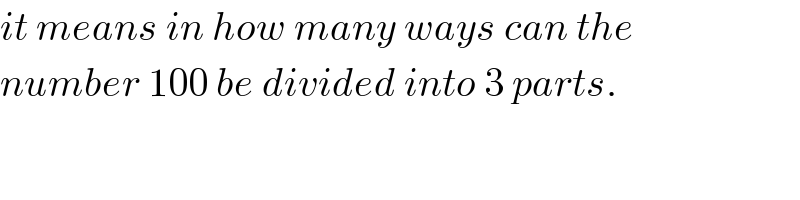
it means in how many ways can the number 100 be divided into 3 parts.
$${it}\:{means}\:{in}\:{how}\:{many}\:{ways}\:{can}\:{the} \\ $$$${number}\:\mathrm{100}\:{be}\:{divided}\:{into}\:\mathrm{3}\:{parts}. \\ $$
Commented by bemath last updated on 18/Jul/20
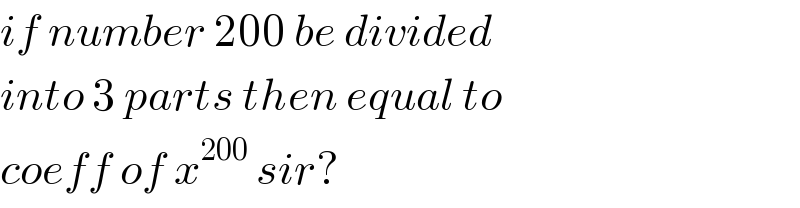
if number 200 be divided into 3 parts then equal to coeff of x^(200) sir?
$${if}\:{number}\:\mathrm{200}\:{be}\:{divided} \\ $$$${into}\:\mathrm{3}\:{parts}\:{then}\:{equal}\:{to} \\ $$$${coeff}\:{of}\:{x}^{\mathrm{200}} \:{sir}? \\ $$
Commented by mr W last updated on 18/Jul/20
yes
$${yes} \\ $$
Commented by bemath last updated on 18/Jul/20
thank you sir. i will learn
$${thank}\:{you}\:{sir}.\:{i}\:{will}\:{learn}\: \\ $$
Commented by prakash jain last updated on 18/Jul/20
Some more ideas around this topic in Wikipedia https://en.m.wikipedia.org/wiki/Partition_(number_theory)

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *