Menu Close

a-cube-ABCD-EFGH-with-length-side-4-cm-Given-point-P-is-midpoint-EF-find-the-distance-of-line-AP-to-line-HB-

Tinku Tara 0 Comments
Pin




Question Number 103945 by bobhans last updated on 18/Jul/20
a cube ABCD.EFGH with length side 4 cm. Given point P is midpoint EF. find the distance of line AP to line HB.
$${a}\:{cube}\:{ABCD}.{EFGH}\:{with}\:{length}\:{side} \\ $$$$\mathrm{4}\:{cm}.\:{Given}\:{point}\:{P}\:{is}\:{midpoint}\:{EF}. \\ $$$${find}\:{the}\:{distance}\:{of}\:{line}\:{AP}\:{to}\:{line} \\ $$$${HB}.\: \\ $$
Answered by bramlex last updated on 18/Jul/20
let : ax+by+cz = −1 be a equation of plane HBP ′ where BP ′ parallel to AP. coordinates A(4,0,0) ; B(4,4,0) ; P ′(4,6,4) and H(0,0,4) (i)substitute B⇒4a+4b = −1 (ii) substitute H⇒4c = −1⇒c =−(1/4) (iii) substitute P ′⇒4a+6b+4c=−1⇒4a+6b = 0 substract (i) &(iii) we get 2b = 1⇒b=(1/2) & a = −(3/4) so eq of plane HBP ′ ⇒−(3/4)x+(1/2)y−(1/4)z+1=0 or −3x+2y−z+4 = 0 so the distance we desired is ((∣−12+4∣)/( (√(9+4+1)))) = (8/( (√(14)))) = ((4(√(14)))/7) cm. ■
$${let}\::\:{ax}+{by}+{cz}\:=\:−\mathrm{1}\:{be}\:{a} \\ $$$${equation}\:{of}\:{plane}\:{HBP}\:'\:{where} \\ $$$${BP}\:'\:{parallel}\:{to}\:{AP}.\: \\ $$$${coordinates}\:{A}\left(\mathrm{4},\mathrm{0},\mathrm{0}\right)\:;\:{B}\left(\mathrm{4},\mathrm{4},\mathrm{0}\right) \\ $$$$;\:{P}\:'\left(\mathrm{4},\mathrm{6},\mathrm{4}\right)\:{and}\:{H}\left(\mathrm{0},\mathrm{0},\mathrm{4}\right) \\ $$$$\left({i}\right){substitute}\:{B}\Rightarrow\mathrm{4}{a}+\mathrm{4}{b}\:=\:−\mathrm{1} \\ $$$$\left({ii}\right)\:{substitute}\:{H}\Rightarrow\mathrm{4}{c}\:=\:−\mathrm{1}\Rightarrow{c}\:=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left({iii}\right)\:{substitute}\:{P} \\ $$$$'\Rightarrow\mathrm{4}{a}+\mathrm{6}{b}+\mathrm{4}{c}=−\mathrm{1}\Rightarrow\mathrm{4}{a}+\mathrm{6}{b}\:=\:\mathrm{0} \\ $$$${substract}\:\left({i}\right)\:\&\left({iii}\right)\: \\ $$$${we}\:{get}\:\mathrm{2}{b}\:=\:\mathrm{1}\Rightarrow{b}=\frac{\mathrm{1}}{\mathrm{2}}\:\&\:{a}\:=\:−\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${so}\:{eq}\:{of}\:{plane}\:{HBP}\:'\:\Rightarrow−\frac{\mathrm{3}}{\mathrm{4}}{x}+\frac{\mathrm{1}}{\mathrm{2}}{y}−\frac{\mathrm{1}}{\mathrm{4}}{z}+\mathrm{1}=\mathrm{0} \\ $$$${or}\:−\mathrm{3}{x}+\mathrm{2}{y}−{z}+\mathrm{4}\:=\:\mathrm{0} \\ $$$${so}\:{the}\:{distance}\:{we}\:{desired}\:{is}\:\frac{\mid−\mathrm{12}+\mathrm{4}\mid}{\:\sqrt{\mathrm{9}+\mathrm{4}+\mathrm{1}}} \\ $$$$=\:\frac{\mathrm{8}}{\:\sqrt{\mathrm{14}}}\:=\:\frac{\mathrm{4}\sqrt{\mathrm{14}}}{\mathrm{7}}\:{cm}.\:\blacksquare\: \\ $$
Commented by bramlex last updated on 18/Jul/20
Commented by bobhans last updated on 18/Jul/20
waw...nice and cooll
$${waw}…{nice}\:{and}\:{cooll} \\ $$
Answered by mr W last updated on 18/Jul/20
Commented by mr W last updated on 18/Jul/20
A(4,0,4) P(4,2,0) H(0,0,0) B(4,4,4) eqn. of AP=(4,0,4)+λ(0,1,−2) eqn. of HB=(0,0,0)+μ(1,1,1) a point on AP is S(4,λ,4−2λ) a point on HB is T(μ,μ,μ) let Φ=ST^2 Φ=(4−μ)^2 +(λ−μ)^2 +(4−2λ−μ)^2 (∂Φ/∂s)=2(λ−μ)+4(2λ+μ−4)=0 ⇒5λ+μ=8 ...(i) (∂Φ/∂t)=−2(4−μ)−2(λ−μ)+2(2λ+μ−4)=0 ⇒λ+3μ=8 ...(ii) ⇒λ=(8/7) ⇒μ=((16)/7) Φ_(min) =(4−((16)/7))^2 +((8/7)−((16)/7))^2 +(4−((16)/7)−((16)/7))^2 =((224)/(49)) min. distance from AP to HB is ST_(min) =(√Φ_(min) )=(√((224)/(49)))=((4(√(14)))/7)
$${A}\left(\mathrm{4},\mathrm{0},\mathrm{4}\right) \\ $$$${P}\left(\mathrm{4},\mathrm{2},\mathrm{0}\right) \\ $$$${H}\left(\mathrm{0},\mathrm{0},\mathrm{0}\right) \\ $$$${B}\left(\mathrm{4},\mathrm{4},\mathrm{4}\right) \\ $$$${eqn}.\:{of}\:{AP}=\left(\mathrm{4},\mathrm{0},\mathrm{4}\right)+\lambda\left(\mathrm{0},\mathrm{1},−\mathrm{2}\right) \\ $$$${eqn}.\:{of}\:{HB}=\left(\mathrm{0},\mathrm{0},\mathrm{0}\right)+\mu\left(\mathrm{1},\mathrm{1},\mathrm{1}\right) \\ $$$${a}\:{point}\:{on}\:{AP}\:{is}\:{S}\left(\mathrm{4},\lambda,\mathrm{4}−\mathrm{2}\lambda\right) \\ $$$${a}\:{point}\:{on}\:{HB}\:{is}\:{T}\left(\mu,\mu,\mu\right) \\ $$$${let}\:\Phi={ST}^{\mathrm{2}} \\ $$$$\Phi=\left(\mathrm{4}−\mu\right)^{\mathrm{2}} +\left(\lambda−\mu\right)^{\mathrm{2}} +\left(\mathrm{4}−\mathrm{2}\lambda−\mu\right)^{\mathrm{2}} \\ $$$$\frac{\partial\Phi}{\partial{s}}=\mathrm{2}\left(\lambda−\mu\right)+\mathrm{4}\left(\mathrm{2}\lambda+\mu−\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}\lambda+\mu=\mathrm{8}\:\:\:…\left({i}\right) \\ $$$$\frac{\partial\Phi}{\partial{t}}=−\mathrm{2}\left(\mathrm{4}−\mu\right)−\mathrm{2}\left(\lambda−\mu\right)+\mathrm{2}\left(\mathrm{2}\lambda+\mu−\mathrm{4}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda+\mathrm{3}\mu=\mathrm{8}\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\lambda=\frac{\mathrm{8}}{\mathrm{7}} \\ $$$$\Rightarrow\mu=\frac{\mathrm{16}}{\mathrm{7}} \\ $$$$\Phi_{{min}} =\left(\mathrm{4}−\frac{\mathrm{16}}{\mathrm{7}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{8}}{\mathrm{7}}−\frac{\mathrm{16}}{\mathrm{7}}\right)^{\mathrm{2}} +\left(\mathrm{4}−\frac{\mathrm{16}}{\mathrm{7}}−\frac{\mathrm{16}}{\mathrm{7}}\right)^{\mathrm{2}} =\frac{\mathrm{224}}{\mathrm{49}} \\ $$$${min}.\:{distance}\:{from}\:{AP}\:{to}\:{HB}\:{is} \\ $$$${ST}_{{min}} =\sqrt{\Phi_{{min}} }=\sqrt{\frac{\mathrm{224}}{\mathrm{49}}}=\frac{\mathrm{4}\sqrt{\mathrm{14}}}{\mathrm{7}} \\ $$
Commented by bobhans last updated on 18/Jul/20
what method it is sir?
$${what}\:{method}\:{it}\:{is}\:{sir}?\: \\ $$
Commented by bobhans last updated on 18/Jul/20
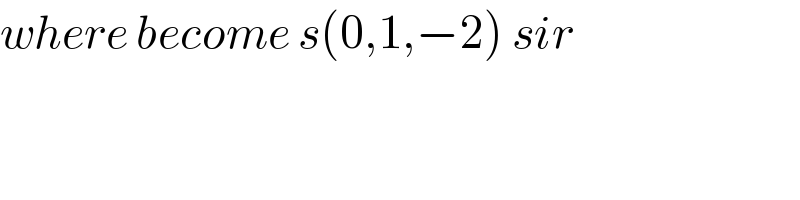
where become s(0,1,−2) sir
$${where}\:{become}\:{s}\left(\mathrm{0},\mathrm{1},−\mathrm{2}\right)\:{sir} \\ $$
Commented by mr W last updated on 18/Jul/20
AP^(→) =(4−4,2−0,0−4)=(0,2,−4) or (0,1,−2)
$$\overset{\rightarrow} {{AP}}=\left(\mathrm{4}−\mathrm{4},\mathrm{2}−\mathrm{0},\mathrm{0}−\mathrm{4}\right)=\left(\mathrm{0},\mathrm{2},−\mathrm{4}\right)\:{or} \\ $$$$\left(\mathrm{0},\mathrm{1},−\mathrm{2}\right) \\ $$
Commented by bramlex last updated on 18/Jul/20
waw...great your method sir.
$${waw}…{great}\:{your}\:{method}\:{sir}.\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *