Question Number 169527 by Giantyusuf last updated on 01/May/22
![evaluate the limit(if it exists) lim_(n→∞) [(((√(n^4 −2n^3 ))−n^2 )/(n+2))]^3](https://www.tinkutara.com/question/Q169527.png)
$$\boldsymbol{{evaluate}}\:\boldsymbol{{the}}\:\boldsymbol{{limit}}\left(\boldsymbol{{if}}\:\boldsymbol{{it}}\:\boldsymbol{{exists}}\right) \\ $$$$\boldsymbol{{lim}}_{\boldsymbol{{n}}\rightarrow\infty} \left[\frac{\sqrt{\boldsymbol{{n}}^{\mathrm{4}} −\mathrm{2}\boldsymbol{{n}}^{\mathrm{3}} }−\boldsymbol{{n}}^{\mathrm{2}} }{\boldsymbol{{n}}+\mathrm{2}}\right]^{\mathrm{3}} \\ $$
Commented by infinityaction last updated on 02/May/22
![p = lim_(n→∞) [((n^2 ((√(1−(2/n))) −1))/(n+2))]^3 use binomail theorem for rational index (1+x)^(n ) = 1+nx+((n(n+1))/(2!))x^2 +..... where −1 ⪇ x⪇1 p = lim_(n→∞) [((1 −(1/n) −1)/((1/n)(1+(2/n))))]^3 p = lim_(n→∞) [ ((−1)/((1+(2/n))))]^3 = −1](https://www.tinkutara.com/question/Q169536.png)
$$\:\:\:\:\:\:\boldsymbol{{p}}\:\:=\:\:\underset{{n}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\:\left[\frac{\boldsymbol{{n}}^{\mathrm{2}} \left(\sqrt{\mathrm{1}−\frac{\mathrm{2}}{\boldsymbol{{n}}}}\:−\mathrm{1}\right)}{\boldsymbol{{n}}+\mathrm{2}}\right]^{\mathrm{3}} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{use}}\:\boldsymbol{\mathrm{binomail}}\:\boldsymbol{\mathrm{theorem}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{rational}}\:\boldsymbol{\mathrm{index}} \\ $$$$\:\:\:\:\:\left(\mathrm{1}+\boldsymbol{\mathrm{x}}\right)^{\boldsymbol{\mathrm{n}}\:\:} =\:\mathrm{1}+\boldsymbol{\mathrm{nx}}+\frac{\boldsymbol{\mathrm{n}}\left(\boldsymbol{\mathrm{n}}+\mathrm{1}\right)}{\mathrm{2}!}\boldsymbol{{x}}^{\mathrm{2}} +…..\:\:\boldsymbol{\mathrm{where}}\:−\mathrm{1}\:\lneq\:\boldsymbol{\mathrm{x}}\lneq\mathrm{1}\: \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{p}}\:\:\:=\:\:\:\:\underset{{n}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\:\:\left[\frac{\mathrm{1}\:−\frac{\mathrm{1}}{\boldsymbol{{n}}}\:\:−\mathrm{1}}{\frac{\mathrm{1}}{\boldsymbol{{n}}}\left(\mathrm{1}+\frac{\mathrm{2}}{\boldsymbol{{n}}}\right)}\right]^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\boldsymbol{{p}}\:\:\:\:=\:\:\:\:\underset{{n}\rightarrow\infty} {\boldsymbol{\mathrm{lim}}}\:\left[\:\frac{−\mathrm{1}}{\left(\mathrm{1}+\frac{\mathrm{2}}{\boldsymbol{{n}}}\right)}\right]^{\mathrm{3}} \:\:\:=\:\:−\mathrm{1} \\ $$
Answered by cortano1 last updated on 02/May/22
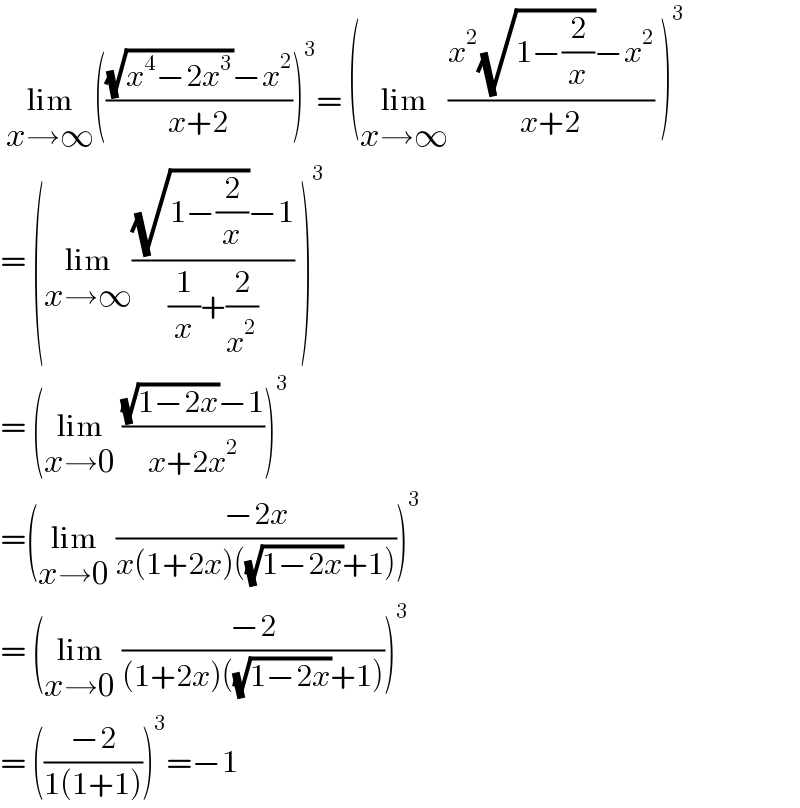
$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\sqrt{{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{3}} }−{x}^{\mathrm{2}} }{{x}+\mathrm{2}}\right)^{\mathrm{3}} =\:\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{\mathrm{2}}{{x}}}−{x}^{\mathrm{2}} }{{x}+\mathrm{2}}\:\right)^{\mathrm{3}} \\ $$$$=\:\left(\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt{\mathrm{1}−\frac{\mathrm{2}}{{x}}}−\mathrm{1}}{\frac{\mathrm{1}}{{x}}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }}\:\right)^{\mathrm{3}} \: \\ $$$$=\:\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{1}−\mathrm{2}{x}}−\mathrm{1}}{{x}+\mathrm{2}{x}^{\mathrm{2}} }\right)^{\mathrm{3}} \\ $$$$=\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2}{x}}{{x}\left(\mathrm{1}+\mathrm{2}{x}\right)\left(\sqrt{\mathrm{1}−\mathrm{2}{x}}+\mathrm{1}\right)}\right)^{\mathrm{3}} \\ $$$$=\:\left(\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2}}{\left(\mathrm{1}+\mathrm{2}{x}\right)\left(\sqrt{\mathrm{1}−\mathrm{2}{x}}+\mathrm{1}\right)}\right)^{\mathrm{3}} \\ $$$$=\:\left(\frac{−\mathrm{2}}{\mathrm{1}\left(\mathrm{1}+\mathrm{1}\right)}\right)^{\mathrm{3}} =−\mathrm{1}\: \\ $$
