Question Number 38466 by maxmathsup by imad last updated on 25/Jun/18
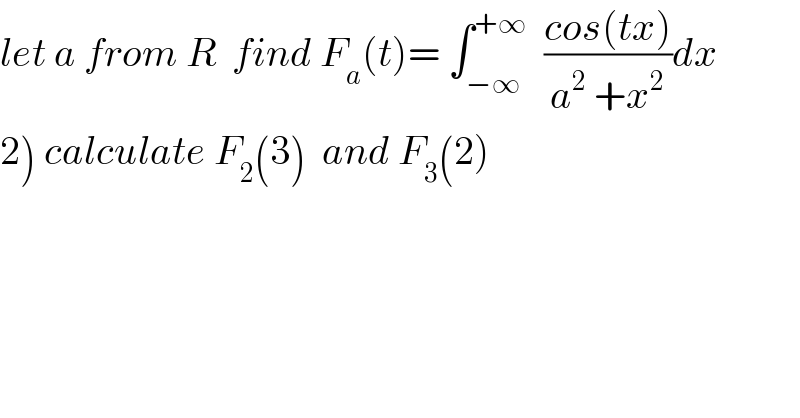
$${let}\:{a}\:{from}\:{R}\:\:{find}\:{F}_{{a}} \left({t}\right)=\:\int_{−\infty} ^{+\infty} \:\:\frac{{cos}\left({tx}\right)}{{a}^{\mathrm{2}} \:+{x}^{\mathrm{2}} }{dx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{F}_{\mathrm{2}} \left(\mathrm{3}\right)\:\:{and}\:{F}_{\mathrm{3}} \left(\mathrm{2}\right) \\ $$
Commented by math khazana by abdo last updated on 27/Jun/18
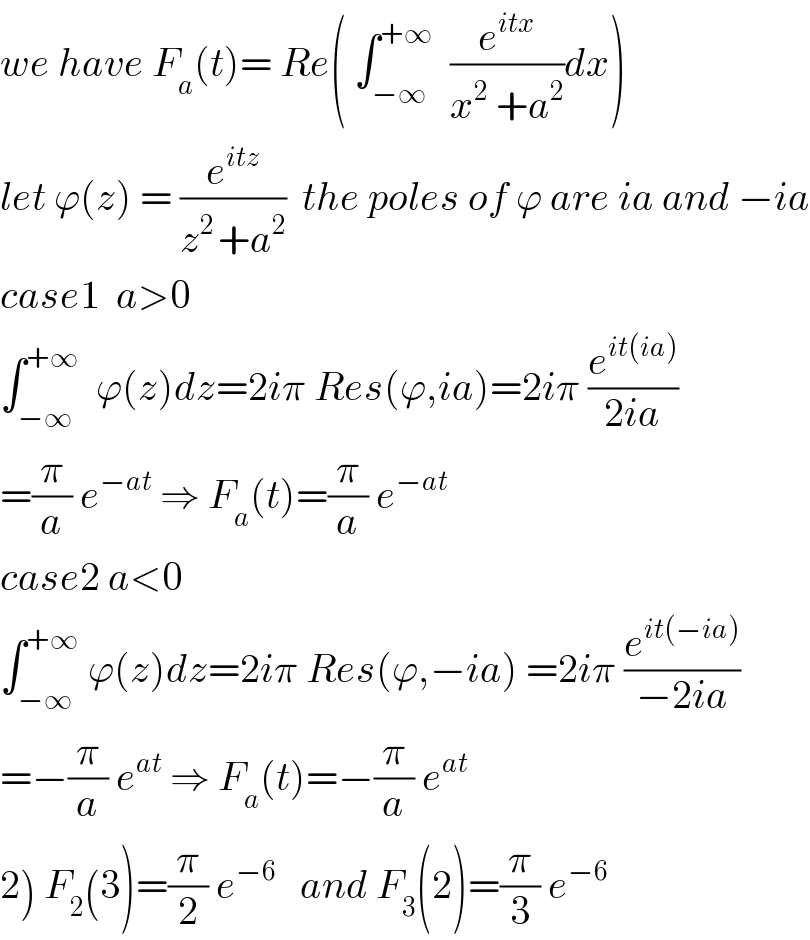
$${we}\:{have}\:{F}_{{a}} \left({t}\right)=\:{Re}\left(\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{itx}} }{{x}^{\mathrm{2}} \:+{a}^{\mathrm{2}} }{dx}\right) \\ $$$${let}\:\varphi\left({z}\right)\:=\:\frac{{e}^{{itz}} }{{z}^{\mathrm{2}\:} +{a}^{\mathrm{2}} }\:\:{the}\:{poles}\:{of}\:\varphi\:{are}\:{ia}\:{and}\:−{ia} \\ $$$${case}\mathrm{1}\:\:{a}>\mathrm{0} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{ia}\right)=\mathrm{2}{i}\pi\:\frac{{e}^{{it}\left({ia}\right)} }{\mathrm{2}{ia}} \\ $$$$=\frac{\pi}{{a}}\:{e}^{−{at}} \:\Rightarrow\:{F}_{{a}} \left({t}\right)=\frac{\pi}{{a}}\:{e}^{−{at}} \\ $$$${case}\mathrm{2}\:{a}<\mathrm{0} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}=\mathrm{2}{i}\pi\:{Res}\left(\varphi,−{ia}\right)\:=\mathrm{2}{i}\pi\:\frac{{e}^{{it}\left(−{ia}\right)} }{−\mathrm{2}{ia}} \\ $$$$=−\frac{\pi}{{a}}\:{e}^{{at}} \:\Rightarrow\:{F}_{{a}} \left({t}\right)=−\frac{\pi}{{a}}\:{e}^{{at}} \\ $$$$\left.\mathrm{2}\right)\:{F}_{\mathrm{2}} \left(\mathrm{3}\right)=\frac{\pi}{\mathrm{2}}\:{e}^{−\mathrm{6}} \:\:\:{and}\:{F}_{\mathrm{3}} \left(\mathrm{2}\right)=\frac{\pi}{\mathrm{3}}\:{e}^{−\mathrm{6}} \\ $$
