Question Number 38488 by Rio Mike last updated on 26/Jun/18
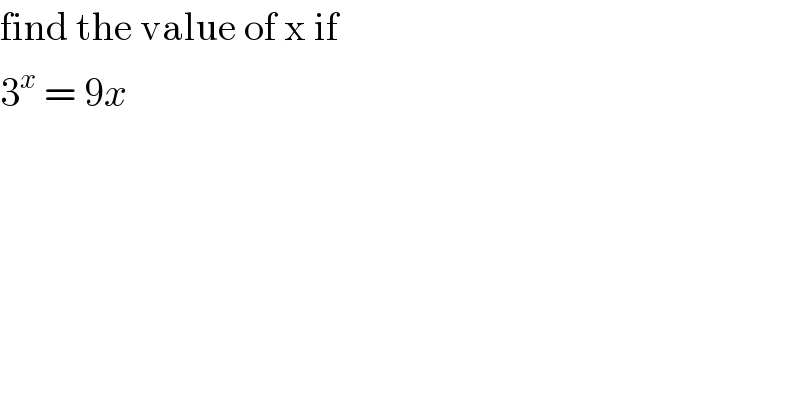
$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}\:\mathrm{if}\: \\ $$$$\mathrm{3}^{{x}} \:=\:\mathrm{9}{x} \\ $$
Answered by $@ty@m last updated on 26/Jun/18

$$\mathrm{3} \\ $$
Answered by MrW3 last updated on 26/Jun/18

$${e}^{{x}\mathrm{ln}\:\mathrm{3}} =\mathrm{9}{x} \\ $$$$\mathrm{1}=\mathrm{9}{xe}^{−{x}\mathrm{ln}\:\mathrm{3}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{9}}=−{xe}^{−{x}\mathrm{ln}\:\mathrm{3}} \\ $$$$−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{9}}=\left(−{x}\mathrm{ln}\:\mathrm{3}\right){e}^{−{x}\mathrm{ln}\:\mathrm{3}} \\ $$$$\Rightarrow−{x}\mathrm{ln}\:\mathrm{3}={W}\left(−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{9}}\right) \\ $$$$\Rightarrow{x}=−\frac{{W}\left(−\frac{\mathrm{ln}\:\mathrm{3}}{\mathrm{9}}\right)}{\mathrm{ln}\:\mathrm{3}}=\begin{cases}{−\frac{−\mathrm{0}.\mathrm{1405}}{\mathrm{ln}\:\mathrm{3}}=\mathrm{0}.\mathrm{1279}}\\{−\frac{−\mathrm{3}.\mathrm{2958}}{\mathrm{ln}\:\mathrm{3}}=\mathrm{3}}\end{cases} \\ $$
Commented by tawa tawa last updated on 26/Jun/18

$$\mathrm{longest}\:\mathrm{time}\:\mathrm{sir}\:\mathrm{Mrw} \\ $$
Commented by MrW3 last updated on 26/Jun/18

$${Yes},\:{but}\:{now}\:{I}'{m}\:{back}. \\ $$
Commented by Rio Mike last updated on 26/Jun/18

$${welcome}\:{sir} \\ $$
Commented by MrW3 last updated on 27/Jun/18

$${thank}\:{you}! \\ $$
Commented by tawa tawa last updated on 28/Jun/18

$$\mathrm{welcome}\:\mathrm{back}\:\mathrm{sir}. \\ $$
