Question Number 104176 by Dwaipayan Shikari last updated on 19/Jul/20
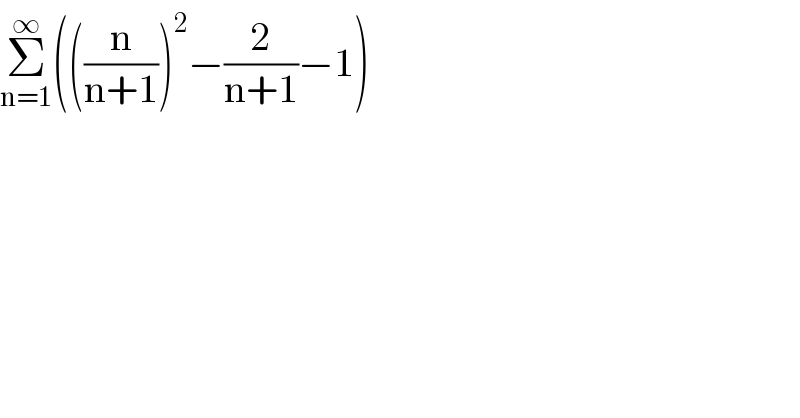
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\left(\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}\right)^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}−\mathrm{1}\right) \\ $$
Answered by OlafThorendsen last updated on 19/Jul/20
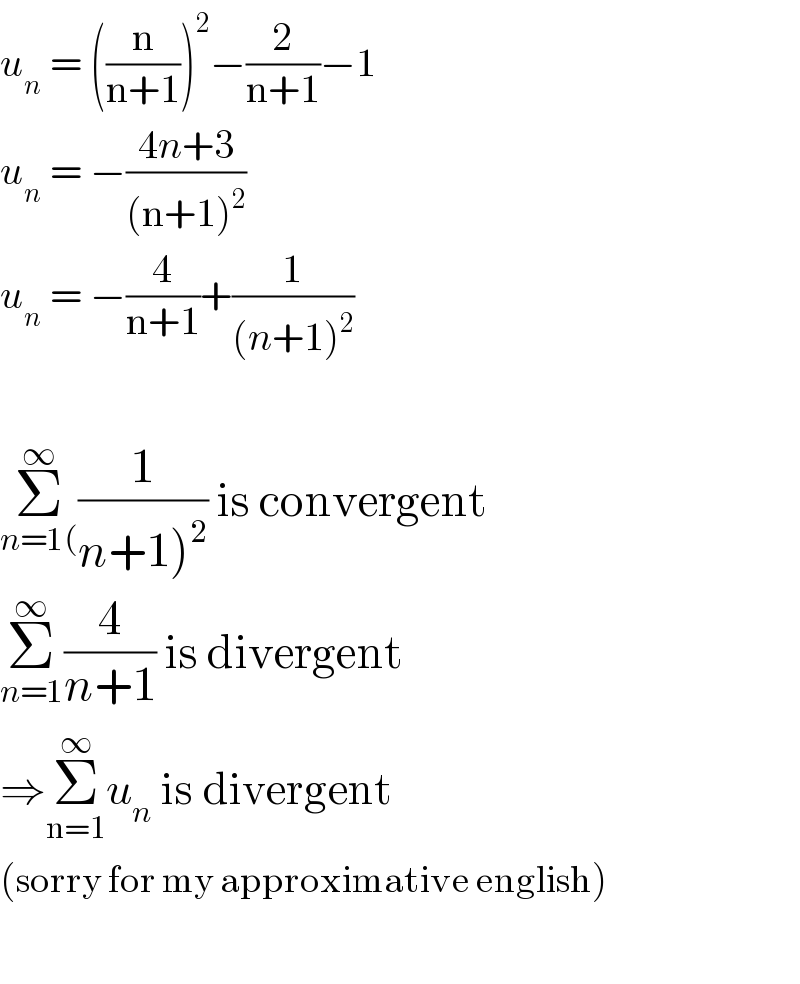
$${u}_{{n}} \:=\:\left(\frac{\mathrm{n}}{\mathrm{n}+\mathrm{1}}\right)^{\mathrm{2}} −\frac{\mathrm{2}}{\mathrm{n}+\mathrm{1}}−\mathrm{1} \\ $$$${u}_{{n}} \:=\:−\frac{\mathrm{4}{n}+\mathrm{3}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${u}_{{n}} \:=\:−\frac{\mathrm{4}}{\mathrm{n}+\mathrm{1}}+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\underset{{n}=\mathrm{1}\left(\right.} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left.{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{convergent} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{4}}{{n}+\mathrm{1}}\:\mathrm{is}\:\mathrm{divergent} \\ $$$$\Rightarrow\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}{u}_{{n}} \:\mathrm{is}\:\mathrm{divergent} \\ $$$$\left(\mathrm{sorry}\:\mathrm{for}\:\mathrm{my}\:\mathrm{approximative}\:\mathrm{english}\right) \\ $$$$ \\ $$
