Question Number 38696 by Sr@2004 last updated on 28/Jun/18
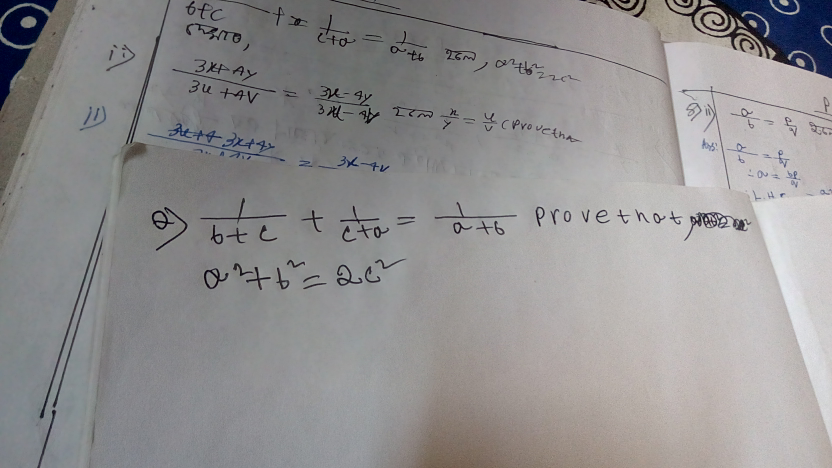
Answered by tanmay.chaudhury50@gmail.com last updated on 28/Jun/18

$$\frac{\mathrm{1}}{{b}+{c}}+\frac{\mathrm{1}}{{c}+{a}}=\frac{\mathrm{2}}{{a}+{b}} \\ $$$$\frac{\mathrm{1}}{{b}+{c}}−\frac{\mathrm{1}}{{a}+{b}}=\frac{\mathrm{1}}{{a}+{b}}−\frac{\mathrm{1}}{{c}+{a}} \\ $$$$\frac{{a}+{b}−{b}−{c}}{\left({a}+{b}\right)\left({b}+{c}\right)}=\frac{{c}+{a}−{a}−{b}}{\left({a}+{b}\right)\left({c}+{a}\right)} \\ $$$$\frac{{a}−{c}}{{b}+{c}}=\frac{{c}−{b}}{{c}+{a}} \\ $$$${a}^{\mathrm{2}} −{c}^{\mathrm{2}} ={c}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{2}{c}^{\mathrm{2}} {proved} \\ $$$${pls}\:{correct}\:{the}\:{question} \\ $$$$ \\ $$
