Menu Close

Question-38699

Tinku Tara 0 Comments
Pin




Question Number 38699 by Tinkutara last updated on 28/Jun/18
Answered by behi83417@gmail.com last updated on 28/Jun/18
y^2 =a^2 +b^2 +2(√((a^2 cos^2 x+b^2 sin^2 x)(a^2 sin^2 x+b^2 cos^2 x))) P=a^2 cos^2 x+b^2 sin^2 x,Q=a^2 sin^2 x+b^2 cos^2 x P+Q=const,PQ,will be max,when: P=Q ⇒a^2 cos^2 x+b^2 sin^2 x=a^2 sin^2 x+b^2 cos^2 x ⇒a^2 cos2x=b^2 cos2x⇒a=b(×) ∨cos2x=0 ⇒y^2 ≤a^2 +b^2 +2(√(((a^2 +b^2 )/2).((a^2 +b^2 )/2)))=2(a^2 +b^2 ) ⇒0<y≤(√(2(a^2 +b^2 ))) .■
$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)\left({a}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\right)} \\ $$$${P}={a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x},{Q}={a}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} {x} \\ $$$${P}+{Q}={const},{PQ},{will}\:{be}\:{max},{when}:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{P}={Q} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}={a}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} {x} \\ $$$$\Rightarrow{a}^{\mathrm{2}} {cos}\mathrm{2}{x}={b}^{\mathrm{2}} {cos}\mathrm{2}{x}\Rightarrow\boldsymbol{{a}}=\boldsymbol{{b}}\left(×\right)\:\vee{cos}\mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow{y}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}}.\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}}}=\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{0}<{y}\leqslant\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}\:\:.\blacksquare \\ $$
Commented by behi83417@gmail.com last updated on 28/Jun/18
dear master:mrW3! thank you so much for solving Q#38032. no message recive to mi from app.so i don't see your answer on this Q.anyway thanks.
Commented by MrW3 last updated on 29/Jun/18
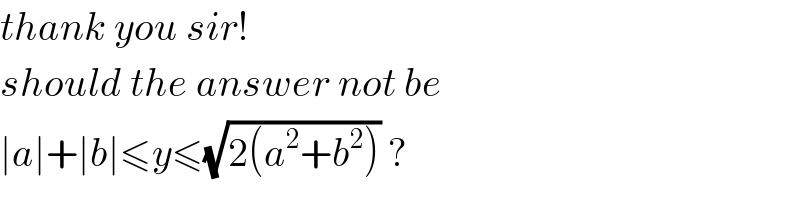
thank you sir! should the answer not be ∣a∣+∣b∣≤y≤(√(2(a^2 +b^2 ))) ?
$${thank}\:{you}\:{sir}! \\ $$$${should}\:{the}\:{answer}\:{not}\:{be} \\ $$$$\mid{a}\mid+\mid{b}\mid\leqslant{y}\leqslant\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}\:? \\ $$
Commented by behi83417@gmail.com last updated on 28/Jun/18
way not! please confirm.
$${way}\:{not}!\:{please}\:{confirm}. \\ $$
Commented by MrW3 last updated on 29/Jun/18
y^2 =a^2 +b^2 +2(√((a^2 cos^2 x+b^2 sin^2 x)(a^2 sin^2 x+b^2 cos^2 x))) y^2 =a^2 +b^2 +2(√((a^4 sin^2 xcos^2 x+a^2 b^2 sin^4 x+a^2 b^2 cos^4 x+b^4 sin^2 xcos^2 x)) y^2 =a^2 +b^2 +2(√((a^4 +b^4 )sin^2 xcos^2 x+a^2 b^2 (sin^4 x+cos^4 x))) y^2 =a^2 +b^2 +2(√((a^4 +b^4 )sin^2 xcos^2 x+a^2 b^2 (sin^4 x+cos^4 x+2sin^2 xcos^2 x)−2a^2 b^2 sin^2 xcos^2 x)) y^2 =a^2 +b^2 +2(√((a^4 +b^4 −2a^2 b^2 )sin^2 xcos^2 x+a^2 b^2 (sin^2 x+cos^2 x)^2 )) y^2 =a^2 +b^2 +2(√((a^2 −b^2 )^2 sin^2 xcos^2 x+a^2 b^2 )) y^2 =a^2 +b^2 +2(√((1/4)(a^2 −b^2 )^2 sin^2 2x+a^2 b^2 )) y^2 =a^2 +b^2 +(√(4a^2 b^2 +(a^2 −b^2 )^2 sin^2 2x)) ⇒y=(√(a^2 +b^2 +(√(4a^2 b^2 +(a^2 −b^2 )^2 sin^2 2x)))) min. y at sin 2x=0: y_(min) =(√(a^2 +b^2 +(√(4a^2 b^2 )))) =(√(a^2 +b^2 +2∣a∣∣b∣))=∣a∣+∣b∣ max. y at sin 2x=±1: y_(max) =(√(a^2 +b^2 +(√(4a^2 b^2 +(a^2 −b^2 )^2 )))) =(√(a^2 +b^2 +(√((a^2 +b^2 )^2 )))) =(√(2(a^2 +b^2 ))) ⇒∣a∣+∣b∣≤y≤(√(2(a^2 +b^2 )))
$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}\right)\left({a}^{\mathrm{2}} {sin}^{\mathrm{2}} {x}+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} {x}\right)} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{4}} \mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} {sin}^{\mathrm{4}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} {cos}^{\mathrm{4}} {x}+{b}^{\mathrm{4}} \mathrm{sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x}\right.} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} \right)\mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}\right)} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} \right)\mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left({sin}^{\mathrm{4}} {x}+{cos}^{\mathrm{4}} {x}+\mathrm{2sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x}\right)−\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:{x}\mathrm{cos}^{\mathrm{2}} \:{x}} \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} −\mathrm{2}{a}^{\mathrm{2}} {b}^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} \left(\mathrm{sin}^{\mathrm{2}} \:{x}+\mathrm{cos}^{\mathrm{2}} \:{x}\right)^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:{xcos}^{\mathrm{2}} {x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\sqrt{\frac{\mathrm{1}}{\mathrm{4}}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} } \\ $$$${y}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}} \\ $$$$\Rightarrow{y}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\mathrm{2}{x}}} \\ $$$${min}.\:{y}\:{at}\:\mathrm{sin}\:\mathrm{2}{x}=\mathrm{0}: \\ $$$${y}_{{min}} =\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} }}\:=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}\mid{a}\mid\mid{b}\mid}=\mid{a}\mid+\mid{b}\mid \\ $$$${max}.\:{y}\:{at}\:\mathrm{sin}\:\mathrm{2}{x}=\pm\mathrm{1}: \\ $$$${y}_{{max}} =\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\mathrm{4}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$$=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\sqrt{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$$=\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$$$ \\ $$$$\Rightarrow\mid{a}\mid+\mid{b}\mid\leqslant{y}\leqslant\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)} \\ $$
Commented by behi83417@gmail.com last updated on 29/Jun/18
perfect!
$${perfect}! \\ $$
Commented by Tinkutara last updated on 29/Jun/18
Ans given is [(a+b),(√(2(a^2 +b^2 )))]
$${Ans}\:{given}\:{is}\:\left[\left({a}+{b}\right),\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)}\right] \\ $$
Commented by Tinkutara last updated on 29/Jun/18
Thank you very much Sir! I got the answer. ��������

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *