Question Number 38743 by kunal1234523 last updated on 29/Jun/18
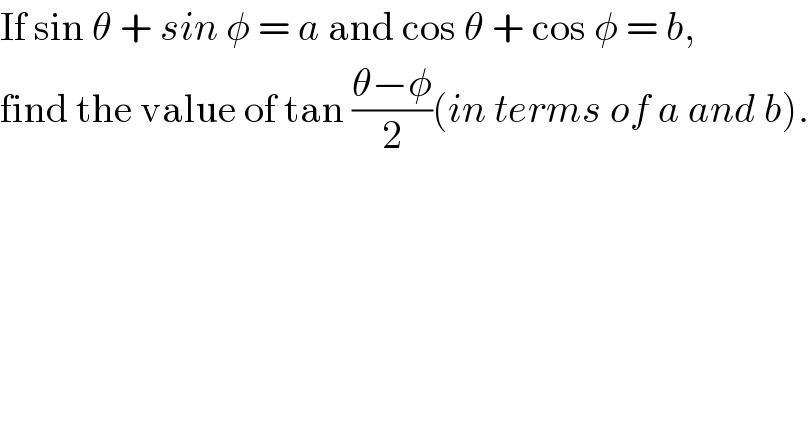
$$\mathrm{If}\:\mathrm{sin}\:\theta\:+\:{sin}\:\phi\:=\:{a}\:\mathrm{and}\:\mathrm{cos}\:\theta\:+\:\mathrm{cos}\:\phi\:=\:{b},\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{tan}\:\frac{\theta−\phi}{\mathrm{2}}\left({in}\:{terms}\:{of}\:{a}\:{and}\:{b}\right). \\ $$
Answered by math1967 last updated on 29/Jun/18

$$\mathrm{sin}\:\theta+\mathrm{sin}\:\phi={a} \\ $$$$\mathrm{2sin}\:\frac{\theta+\phi}{\mathrm{2}}\mathrm{cos}\:\frac{\theta−\phi}{\mathrm{2}}={a} \\ $$$$\mathrm{cos}\:\theta+\mathrm{cos}\:\phi={b} \\ $$$$\mathrm{2cos}\:\frac{\theta+\phi}{\mathrm{2}}\mathrm{cos}\:\frac{\theta−\phi}{\mathrm{2}}={b} \\ $$$$\mathrm{4cos}\:^{\mathrm{2}} \frac{\theta−\phi}{\mathrm{2}}\left({sin}^{\mathrm{2}} \frac{\theta+\phi}{\mathrm{2}}+{cos}^{\mathrm{2}} \frac{\theta+\phi}{\mathrm{2}}\right)={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${cos}^{\mathrm{2}} \frac{\theta−\phi}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${sec}^{\mathrm{2}} \frac{\theta−\phi}{\mathrm{2}}=\frac{\mathrm{4}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\therefore{tan}\frac{\theta−\phi}{\mathrm{2}}=\sqrt{\frac{\mathrm{4}−{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$
Commented by kunal1234523 last updated on 29/Jun/18

$${thank}\:{you}\:{sir} \\ $$
