Question Number 169918 by pticantor last updated on 12/May/22
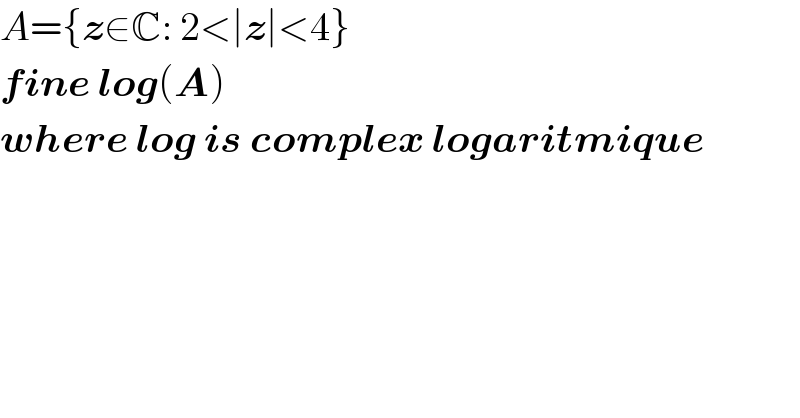
$${A}=\left\{\boldsymbol{{z}}\in\mathbb{C}:\:\mathrm{2}<\mid\boldsymbol{{z}}\mid<\mathrm{4}\right\} \\ $$$$\boldsymbol{{fine}}\:\boldsymbol{{log}}\left(\boldsymbol{{A}}\right) \\ $$$$\boldsymbol{{where}}\:\boldsymbol{{log}}\:\boldsymbol{{is}}\:\boldsymbol{{complex}}\:\boldsymbol{{logaritmique}} \\ $$
Answered by pticantor last updated on 12/May/22

$$\boldsymbol{{besoin}}\:\boldsymbol{{d}}'\boldsymbol{{aide}}\:\boldsymbol{{please}}!! \\ $$
Answered by Mathspace last updated on 12/May/22

$${what}\:{mean}\:{logA}\:… \\ $$
Commented by pticantor last updated on 13/May/22
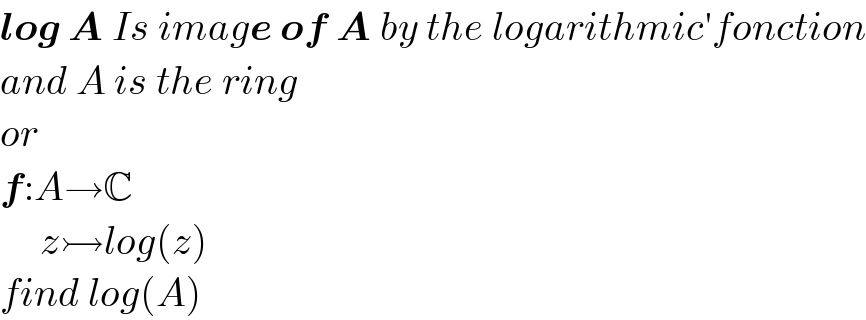
$$\boldsymbol{{log}}\:\boldsymbol{{A}}\:{Is}\:{imag}\boldsymbol{{e}}\:\boldsymbol{{of}}\:\boldsymbol{{A}}\:{by}\:{the}\:{logarithmic}'{fonction} \\ $$$${and}\:{A}\:{is}\:{the}\:{ring}\: \\ $$$${or}\: \\ $$$$\boldsymbol{{f}}:{A}\rightarrow\mathbb{C} \\ $$$$\:\:\:\:\:{z}\rightarrowtail{log}\left({z}\right) \\ $$$${find}\:{log}\left({A}\right) \\ $$
Answered by Mathspace last updated on 13/May/22

$${if}\:{z}={re}^{{i}\theta} \:\Rightarrow\mid{z}\mid={r}\Rightarrow\mathrm{2}<{r}<\mathrm{4} \\ $$$${and}\:{logz}={logr}+{i}\left(\theta+\mathrm{2}{k}\pi\right)\:\Rightarrow \\ $$$${logA}=\left\{{logr}+{i}\left(\theta+\mathrm{2}{k}\pi\right)\:/{k}\in{Z}\right\} \\ $$$${une}\:{determination}\:{principale}\:{est} \\ $$$${logr}+{i}\theta\:\:\:\:\:−\pi<\theta<\pi \\ $$$$ \\ $$
Commented by pticantor last updated on 13/May/22

$$\boldsymbol{{je}}\:\boldsymbol{{crois}}\:\boldsymbol{{que}}\:\boldsymbol{{vous}}\:\boldsymbol{{avez}}\:\boldsymbol{{juste}}\:\boldsymbol{{donner}} \\ $$$$\boldsymbol{{la}}\:\boldsymbol{{definition}}\:\boldsymbol{{du}}\:\boldsymbol{{logarithme}}\:\boldsymbol{{complex}}! \\ $$$$\boldsymbol{{mais}}\:\boldsymbol{{on}}\:\boldsymbol{{me}}\:\boldsymbol{{demande}}\:\boldsymbol{{la}}\:\boldsymbol{{nature}}\:\boldsymbol{{de}}\:\boldsymbol{{log}}\left(\boldsymbol{{A}}\right)\:{e}\boldsymbol{{t}}\:\boldsymbol{{le}}\: \\ $$$$\boldsymbol{{tracage}}\:\boldsymbol{{de}}\:\boldsymbol{{la}}\:\boldsymbol{{courbe}} \\ $$
