Menu Close

tan-1-a-x-b-c-dx-

Tinku Tara 0 Comments
Pin




Question Number 104718 by  M±th+et+s last updated on 23/Jul/20
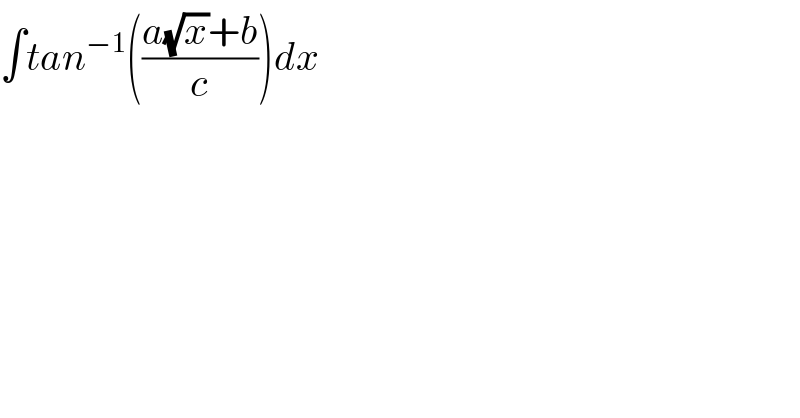
∫tan^(−1) (((a(√x)+b)/c))dx
$$\int{tan}^{−\mathrm{1}} \left(\frac{{a}\sqrt{{x}}+{b}}{{c}}\right){dx}\: \\ $$
Answered by Dwaipayan Shikari last updated on 23/Jul/20
∫((2c(√x))/a)tan^(−1) udu u=((a(√x)+b)/c)⇒(a/(2c(√x)))=(du/dx) ((2c)/a)∫(√x)tan^(−1) du (√x)=((cu−b)/a) ((2c)/a)∫(((cu)/a)−(b/a))tan^(−1) udu ((2c^2 )/a^2 )∫utan^(−1) u−((2bc)/a^2 )∫tan^(−1) udu ∫utan^(−1) u=(u^2 /2)tan^(−1) u−(1/2)∫(u^2 /(u^2 +1))=(u^2 /2)tan^(−1) u−(u/2)−(1/2)tan^(−1) u ∫tan^(−1) udu=utan^(−1) u−(1/2)log(u^2 +1) ((2c^2 )/a^2 )((u^2 /2)tan^(−1) u−(u/2)−(1/2)tan^(−1) u)−((2bc)/a^2 )(utan^(−1) u−(1/2)log(u^2 +1))+C ((2c^2 )/a^2 )((((((a(√x)+b)/c))^2 )/2)tan^(−1) (((a(√x)+b)/c))−((a(√x)+b)/(2c))−(1/2)tan^(−1) (((a(√x)+b)/c)))+ (−((2bc)/a^2 )(((a(√x)+b)/c)tan^(−1) (((a(√x)+b)/c))−(1/2)log((((a(√x)+b)/c))^2 +1))+C
$$\int\frac{\mathrm{2}{c}\sqrt{{x}}}{{a}}{tan}^{−\mathrm{1}} {udu}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{u}=\frac{{a}\sqrt{{x}}+{b}}{{c}}\Rightarrow\frac{{a}}{\mathrm{2}{c}\sqrt{{x}}}=\frac{{du}}{{dx}} \\ $$$$\frac{\mathrm{2}{c}}{{a}}\int\sqrt{{x}}{tan}^{−\mathrm{1}} {du}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{{x}}=\frac{{cu}−{b}}{{a}} \\ $$$$\frac{\mathrm{2}{c}}{{a}}\int\left(\frac{{cu}}{{a}}−\frac{{b}}{{a}}\right){tan}^{−\mathrm{1}} {udu} \\ $$$$\frac{\mathrm{2}{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\int{utan}^{−\mathrm{1}} {u}−\frac{\mathrm{2}{bc}}{{a}^{\mathrm{2}} }\int{tan}^{−\mathrm{1}} {udu} \\ $$$$\int{utan}^{−\mathrm{1}} {u}=\frac{{u}^{\mathrm{2}} }{\mathrm{2}}{tan}^{−\mathrm{1}} {u}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{2}} +\mathrm{1}}=\frac{{u}^{\mathrm{2}} }{\mathrm{2}}{tan}^{−\mathrm{1}} {u}−\frac{{u}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} {u} \\ $$$$\int{tan}^{−\mathrm{1}} {udu}={utan}^{−\mathrm{1}} {u}−\frac{\mathrm{1}}{\mathrm{2}}{log}\left({u}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\frac{\mathrm{2}{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{{u}^{\mathrm{2}} }{\mathrm{2}}{tan}^{−\mathrm{1}} {u}−\frac{{u}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} {u}\right)−\frac{\mathrm{2}{bc}}{{a}^{\mathrm{2}} }\left({utan}^{−\mathrm{1}} {u}−\frac{\mathrm{1}}{\mathrm{2}}{log}\left({u}^{\mathrm{2}} +\mathrm{1}\right)\right)+{C} \\ $$$$\frac{\mathrm{2}{c}^{\mathrm{2}} }{{a}^{\mathrm{2}} }\left(\frac{\left(\frac{{a}\sqrt{{x}}+{b}}{{c}}\right)^{\mathrm{2}} }{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{{a}\sqrt{{x}}+{b}}{{c}}\right)−\frac{{a}\sqrt{{x}}+{b}}{\mathrm{2}{c}}−\frac{\mathrm{1}}{\mathrm{2}}{tan}^{−\mathrm{1}} \left(\frac{{a}\sqrt{{x}}+{b}}{{c}}\right)\right)+ \\ $$$$\left(−\frac{\mathrm{2}{bc}}{{a}^{\mathrm{2}} }\left(\frac{{a}\sqrt{{x}}+{b}}{{c}}{tan}^{−\mathrm{1}} \left(\frac{{a}\sqrt{{x}}+{b}}{{c}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{log}\left(\left(\frac{{a}\sqrt{{x}}+{b}}{{c}}\right)^{\mathrm{2}} +\mathrm{1}\right)\right)+{C}\right. \\ $$
Commented by  M±th+et+s last updated on 23/Jul/20
well done
$${well}\:{done}\: \\ $$
Answered by mathmax by abdo last updated on 24/Jul/20
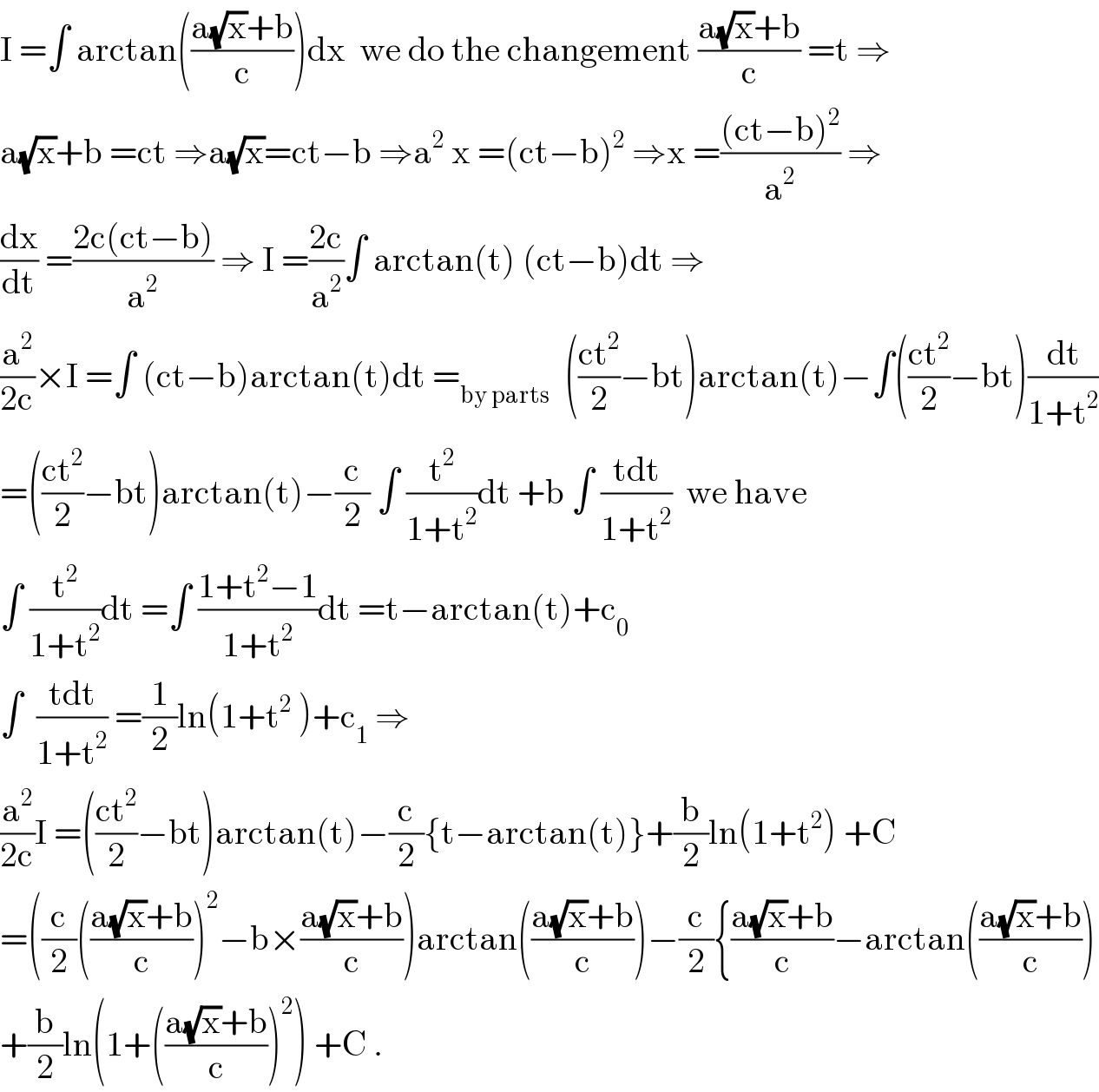
I =∫ arctan(((a(√x)+b)/c))dx we do the changement ((a(√x)+b)/c) =t ⇒ a(√x)+b =ct ⇒a(√x)=ct−b ⇒a^2 x =(ct−b)^2 ⇒x =(((ct−b)^2 )/a^2 ) ⇒ (dx/dt) =((2c(ct−b))/a^2 ) ⇒ I =((2c)/a^2 )∫ arctan(t) (ct−b)dt ⇒ (a^2 /(2c))×I =∫ (ct−b)arctan(t)dt =_(by parts) (((ct^2 )/2)−bt)arctan(t)−∫(((ct^2 )/2)−bt)(dt/(1+t^2 )) =(((ct^2 )/2)−bt)arctan(t)−(c/2) ∫ (t^2 /(1+t^2 ))dt +b ∫ ((tdt)/(1+t^2 )) we have ∫ (t^2 /(1+t^2 ))dt =∫ ((1+t^2 −1)/(1+t^2 ))dt =t−arctan(t)+c_0 ∫ ((tdt)/(1+t^2 )) =(1/2)ln(1+t^2 )+c_1 ⇒ (a^2 /(2c))I =(((ct^2 )/2)−bt)arctan(t)−(c/2){t−arctan(t)}+(b/2)ln(1+t^2 ) +C =((c/2)(((a(√x)+b)/c))^2 −b×((a(√x)+b)/c))arctan(((a(√x)+b)/c))−(c/2){((a(√x)+b)/c)−arctan(((a(√x)+b)/c)) +(b/2)ln(1+(((a(√x)+b)/c))^2 ) +C .
$$\mathrm{I}\:=\int\:\mathrm{arctan}\left(\frac{\mathrm{a}\sqrt{\mathrm{x}}+\mathrm{b}}{\mathrm{c}}\right)\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{a}\sqrt{\mathrm{x}}+\mathrm{b}}{\mathrm{c}}\:=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{a}\sqrt{\mathrm{x}}+\mathrm{b}\:=\mathrm{ct}\:\Rightarrow\mathrm{a}\sqrt{\mathrm{x}}=\mathrm{ct}−\mathrm{b}\:\Rightarrow\mathrm{a}^{\mathrm{2}} \:\mathrm{x}\:=\left(\mathrm{ct}−\mathrm{b}\right)^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\frac{\left(\mathrm{ct}−\mathrm{b}\right)^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{dx}}{\mathrm{dt}}\:=\frac{\mathrm{2c}\left(\mathrm{ct}−\mathrm{b}\right)}{\mathrm{a}^{\mathrm{2}} }\:\Rightarrow\:\mathrm{I}\:=\frac{\mathrm{2c}}{\mathrm{a}^{\mathrm{2}} }\int\:\mathrm{arctan}\left(\mathrm{t}\right)\:\left(\mathrm{ct}−\mathrm{b}\right)\mathrm{dt}\:\Rightarrow \\ $$$$\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2c}}×\mathrm{I}\:=\int\:\left(\mathrm{ct}−\mathrm{b}\right)\mathrm{arctan}\left(\mathrm{t}\right)\mathrm{dt}\:=_{\mathrm{by}\:\mathrm{parts}} \:\:\left(\frac{\mathrm{ct}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{bt}\right)\mathrm{arctan}\left(\mathrm{t}\right)−\int\left(\frac{\mathrm{ct}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{bt}\right)\frac{\mathrm{dt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} } \\ $$$$=\left(\frac{\mathrm{ct}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{bt}\right)\mathrm{arctan}\left(\mathrm{t}\right)−\frac{\mathrm{c}}{\mathrm{2}}\:\int\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:+\mathrm{b}\:\int\:\frac{\mathrm{tdt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\int\:\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:=\mathrm{t}−\mathrm{arctan}\left(\mathrm{t}\right)+\mathrm{c}_{\mathrm{0}} \\ $$$$\int\:\:\frac{\mathrm{tdt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \:\right)+\mathrm{c}_{\mathrm{1}} \:\Rightarrow \\ $$$$\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2c}}\mathrm{I}\:=\left(\frac{\mathrm{ct}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{bt}\right)\mathrm{arctan}\left(\mathrm{t}\right)−\frac{\mathrm{c}}{\mathrm{2}}\left\{\mathrm{t}−\mathrm{arctan}\left(\mathrm{t}\right)\right\}+\frac{\mathrm{b}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\:+\mathrm{C} \\ $$$$=\left(\frac{\mathrm{c}}{\mathrm{2}}\left(\frac{\mathrm{a}\sqrt{\mathrm{x}}+\mathrm{b}}{\mathrm{c}}\right)^{\mathrm{2}} −\mathrm{b}×\frac{\mathrm{a}\sqrt{\mathrm{x}}+\mathrm{b}}{\mathrm{c}}\right)\mathrm{arctan}\left(\frac{\mathrm{a}\sqrt{\mathrm{x}}+\mathrm{b}}{\mathrm{c}}\right)−\frac{\mathrm{c}}{\mathrm{2}}\left\{\frac{\mathrm{a}\sqrt{\mathrm{x}}+\mathrm{b}}{\mathrm{c}}−\mathrm{arctan}\left(\frac{\mathrm{a}\sqrt{\mathrm{x}}+\mathrm{b}}{\mathrm{c}}\right)\right. \\ $$$$+\frac{\mathrm{b}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\left(\frac{\mathrm{a}\sqrt{\mathrm{x}}+\mathrm{b}}{\mathrm{c}}\right)^{\mathrm{2}} \right)\:+\mathrm{C}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *