Question Number 39267 by ajfour last updated on 04/Jul/18

Commented by ajfour last updated on 04/Jul/18
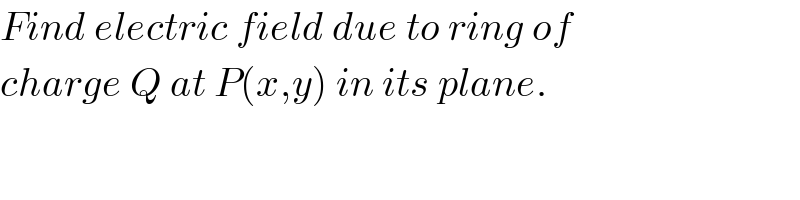
$${Find}\:{electric}\:{field}\:{due}\:{to}\:{ring}\:{of} \\ $$$${charge}\:{Q}\:{at}\:{P}\left({x},{y}\right)\:{in}\:{its}\:{plane}. \\ $$
Answered by ajfour last updated on 04/Jul/18
![E^� = ∮((dQ(r^� −R^� ))/(4πε_0 ∣r^� −R^� ∣^3 )) =(Q/(4πε_0 (2π)))∮(((x−Rcos θ)i^� +(y−Rsin θ)j^� )/([(x−Rcos θ)^2 +(y−Rsin θ)^2 ]^(3/2) ))dθ let x= rcos φ, y=rsin φ E^� = (Q/(8π^2 ε_0 ))[(∮(((rcos φ−Rcos θ)dθ)/([r^2 +R^2 −2rRcos (θ−φ)]^(3/2) )))i^� +(∮(((rsin φ−Rsin θ)dθ)/([r^2 +R^2 −2rRcos (θ−φ)]^(3/2) )))j^� ] ..... please help..](https://www.tinkutara.com/question/Q39271.png)
$$\bar {{E}}\:=\:\oint\frac{{dQ}\left(\bar {{r}}−\bar {{R}}\right)}{\mathrm{4}\pi\epsilon_{\mathrm{0}} \mid\bar {{r}}−\bar {{R}}\mid^{\mathrm{3}} } \\ $$$$\:\:\:\:=\frac{{Q}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} \left(\mathrm{2}\pi\right)}\oint\frac{\left({x}−{R}\mathrm{cos}\:\theta\right)\hat {{i}}+\left({y}−{R}\mathrm{sin}\:\theta\right)\hat {{j}}}{\left[\left({x}−{R}\mathrm{cos}\:\theta\right)^{\mathrm{2}} +\left({y}−{R}\mathrm{sin}\:\theta\right)^{\mathrm{2}} \right]^{\mathrm{3}/\mathrm{2}} }{d}\theta\: \\ $$$${let}\:\:{x}=\:{r}\mathrm{cos}\:\phi,\:\:{y}={r}\mathrm{sin}\:\phi \\ $$$$\:\:\bar {{E}}\:=\:\frac{{Q}}{\mathrm{8}\pi^{\mathrm{2}} \epsilon_{\mathrm{0}} }\left[\left(\oint\frac{\left({r}\mathrm{cos}\:\phi−{R}\mathrm{cos}\:\theta\right){d}\theta}{\left[{r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\left(\theta−\phi\right)\right]^{\mathrm{3}/\mathrm{2}} }\right)\hat {{i}}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:+\left(\oint\frac{\left({r}\mathrm{sin}\:\phi−{R}\mathrm{sin}\:\theta\right){d}\theta}{\left[{r}^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}{rR}\mathrm{cos}\:\left(\theta−\phi\right)\right]^{\mathrm{3}/\mathrm{2}} }\right)\hat {{j}}\:\right] \\ $$$$\:….. \\ $$$${please}\:{help}.. \\ $$
