Question Number 104858 by ~blr237~ last updated on 24/Jul/20
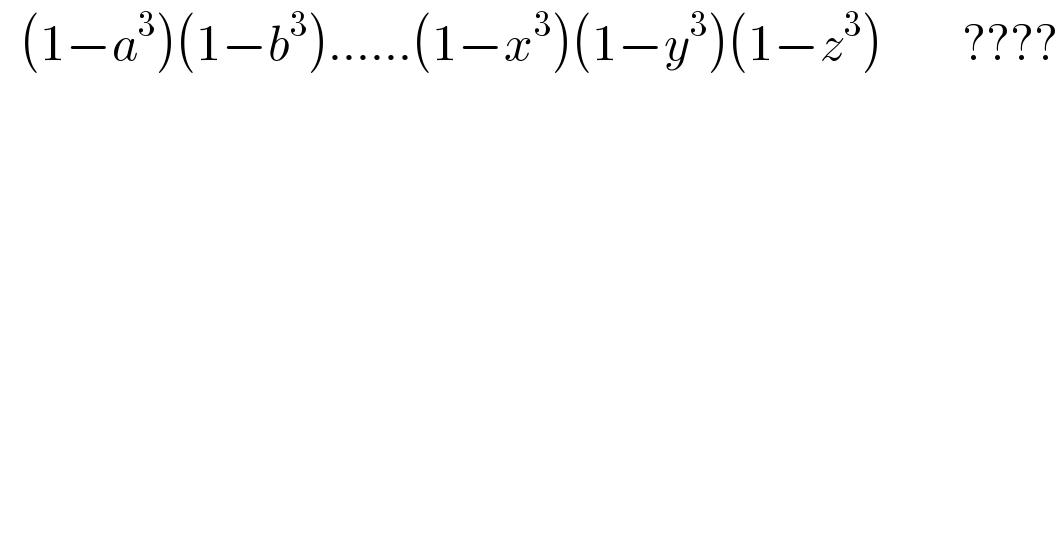
$$\:\:\left(\mathrm{1}−{a}^{\mathrm{3}} \right)\left(\mathrm{1}−{b}^{\mathrm{3}} \right)……\left(\mathrm{1}−{x}^{\mathrm{3}} \right)\left(\mathrm{1}−{y}^{\mathrm{3}} \right)\left(\mathrm{1}−{z}^{\mathrm{3}} \right)\:\:\:\:\:\:\:\:???? \\ $$
Commented by 1549442205PVT last updated on 24/Jul/20

$$\boldsymbol{\mathrm{what}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{your}}\:\:\boldsymbol{\mathrm{question}}? \\ $$
Answered by ~blr237~ last updated on 24/Jul/20
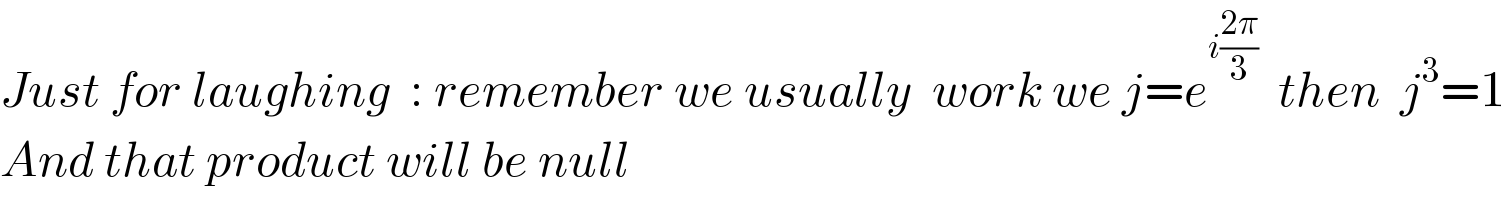
$${Just}\:{for}\:{laughing}\:\::\:{remember}\:{we}\:{usually}\:\:{work}\:{we}\:{j}={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:{then}\:\:{j}^{\mathrm{3}} =\mathrm{1} \\ $$$${And}\:{that}\:{product}\:{will}\:{be}\:{null} \\ $$
Commented by 1549442205PVT last updated on 25/Jul/20
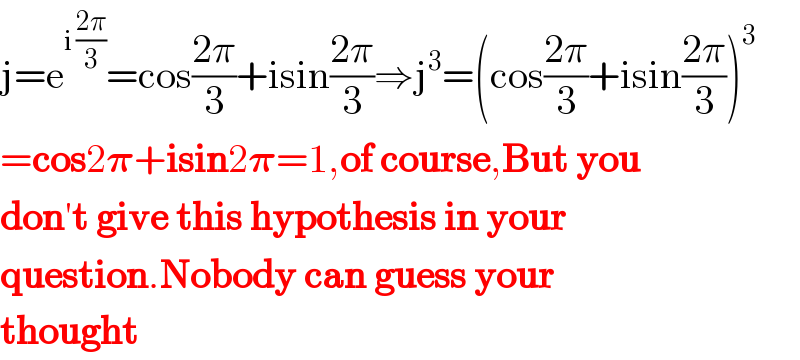
$$\mathrm{j}=\mathrm{e}^{\mathrm{i}\:\frac{\mathrm{2}\pi}{\mathrm{3}}} =\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{isin}\frac{\mathrm{2}\pi}{\mathrm{3}}\Rightarrow\mathrm{j}^{\mathrm{3}} =\left(\mathrm{cos}\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{isin}\frac{\mathrm{2}\pi}{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$$=\boldsymbol{\mathrm{cos}}\mathrm{2}\boldsymbol{\pi}+\boldsymbol{\mathrm{isin}}\mathrm{2}\boldsymbol{\pi}=\mathrm{1},\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{course}},\boldsymbol{\mathrm{But}}\:\boldsymbol{\mathrm{you}} \\ $$$$\boldsymbol{\mathrm{don}}'\boldsymbol{\mathrm{t}}\:\boldsymbol{\mathrm{give}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{hypothesis}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{your}} \\ $$$$\boldsymbol{\mathrm{question}}.\boldsymbol{\mathrm{Nobody}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{guess}}\:\boldsymbol{\mathrm{your}} \\ $$$$\boldsymbol{\mathrm{thought}} \\ $$
