Menu Close

let-F-t-0-sinx-x-1-x-2-e-tx-1-x-2-dx-witht-0-1-caculate-dF-dt-t-2-find-a-simple-form-of-F-t-3-find-the-value-of-0-sinx-x-1-x-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 39368 by maxmathsup by imad last updated on 05/Jul/18
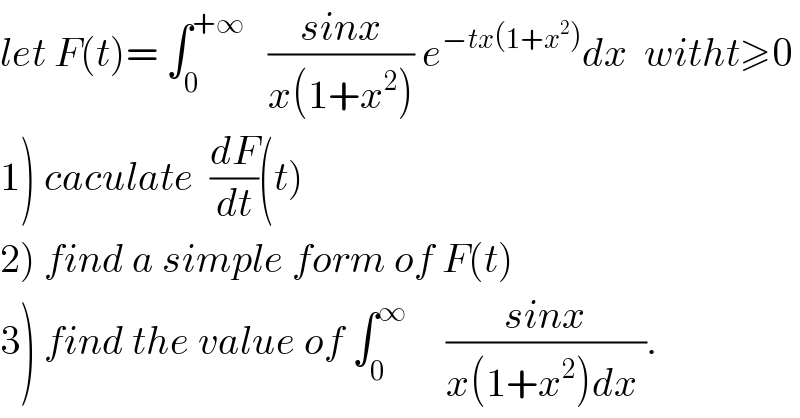
let F(t)= ∫_0 ^(+∞) ((sinx)/(x(1+x^2 ))) e^(−tx(1+x^2 )) dx witht≥0 1) caculate (dF/dt)(t) 2) find a simple form of F(t) 3) find the value of ∫_0 ^∞ ((sinx)/(x(1+x^2 )dx )).
$${let}\:{F}\left({t}\right)=\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\frac{{sinx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:{e}^{−{tx}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} {dx}\:\:{witht}\geqslant\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{caculate}\:\:\frac{{dF}}{{dt}}\left({t}\right) \\ $$$$\left.\mathrm{2}\right)\:{find}\:{a}\:{simple}\:{form}\:{of}\:{F}\left({t}\right) \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{sinx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:}. \\ $$
Commented by math khazana by abdo last updated on 08/Jul/18
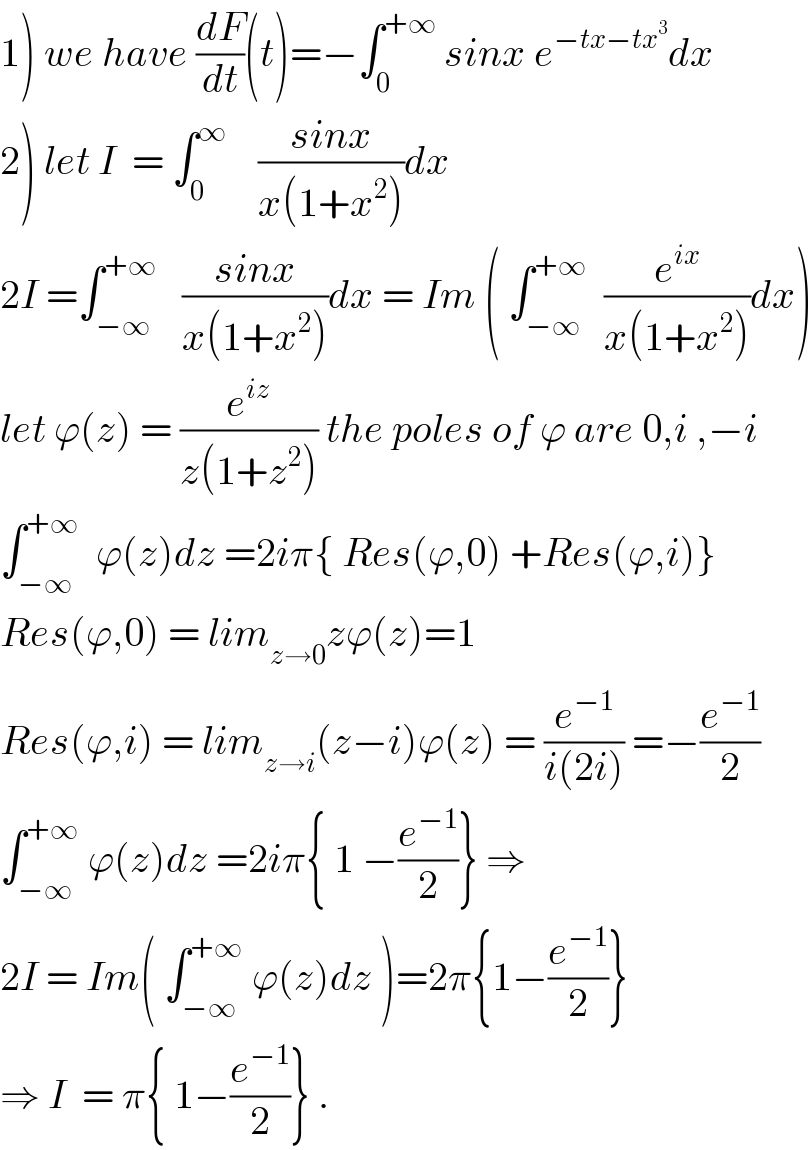
1) we have (dF/dt)(t)=−∫_0 ^(+∞) sinx e^(−tx−tx^3 ) dx 2) let I = ∫_0 ^∞ ((sinx)/(x(1+x^2 )))dx 2I =∫_(−∞) ^(+∞) ((sinx)/(x(1+x^2 )))dx = Im ( ∫_(−∞) ^(+∞) (e^(ix) /(x(1+x^2 )))dx) let ϕ(z) = (e^(iz) /(z(1+z^2 ))) the poles of ϕ are 0,i ,−i ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,0) +Res(ϕ,i)} Res(ϕ,0) = lim_(z→0) zϕ(z)=1 Res(ϕ,i) = lim_(z→i) (z−i)ϕ(z) = (e^(−1) /(i(2i))) =−(e^(−1) /2) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ 1 −(e^(−1) /2)} ⇒ 2I = Im( ∫_(−∞) ^(+∞) ϕ(z)dz )=2π{1−(e^(−1) /2)} ⇒ I = π{ 1−(e^(−1) /2)} .
$$\left.\mathrm{1}\right)\:{we}\:{have}\:\frac{{dF}}{{dt}}\left({t}\right)=−\int_{\mathrm{0}} ^{+\infty} \:{sinx}\:{e}^{−{tx}−{tx}^{\mathrm{3}} } {dx} \\ $$$$\left.\mathrm{2}\right)\:{let}\:{I}\:\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{sinx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\:\:\frac{{sinx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}\:=\:{Im}\:\left(\:\int_{−\infty} ^{+\infty} \:\:\frac{{e}^{{ix}} }{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}\right) \\ $$$${let}\:\varphi\left({z}\right)\:=\:\frac{{e}^{{iz}} }{{z}\left(\mathrm{1}+{z}^{\mathrm{2}} \right)}\:{the}\:{poles}\:{of}\:\varphi\:{are}\:\mathrm{0},{i}\:,−{i} \\ $$$$\int_{−\infty} ^{+\infty} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,\mathrm{0}\right)\:+{Res}\left(\varphi,{i}\right)\right\} \\ $$$${Res}\left(\varphi,\mathrm{0}\right)\:=\:{lim}_{{z}\rightarrow\mathrm{0}} {z}\varphi\left({z}\right)=\mathrm{1} \\ $$$${Res}\left(\varphi,{i}\right)\:=\:{lim}_{{z}\rightarrow{i}} \left({z}−{i}\right)\varphi\left({z}\right)\:=\:\frac{{e}^{−\mathrm{1}} }{{i}\left(\mathrm{2}{i}\right)}\:=−\frac{{e}^{−\mathrm{1}} }{\mathrm{2}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:\mathrm{1}\:−\frac{{e}^{−\mathrm{1}} }{\mathrm{2}}\right\}\:\Rightarrow \\ $$$$\mathrm{2}{I}\:=\:{Im}\left(\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:\right)=\mathrm{2}\pi\left\{\mathrm{1}−\frac{{e}^{−\mathrm{1}} }{\mathrm{2}}\right\} \\ $$$$\Rightarrow\:{I}\:\:=\:\pi\left\{\:\mathrm{1}−\frac{{e}^{−\mathrm{1}} }{\mathrm{2}}\right\}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *