Menu Close

The-values-of-a-for-which-y-ax-2-ax-1-24-and-x-ay-2-ay-1-24-touch-each-other-are-1-2-3-2-3-2-3-13-601-12-4-13-601-12-

Tinku Tara 0 Comments
Pin




Question Number 39384 by rahul 19 last updated on 05/Jul/18
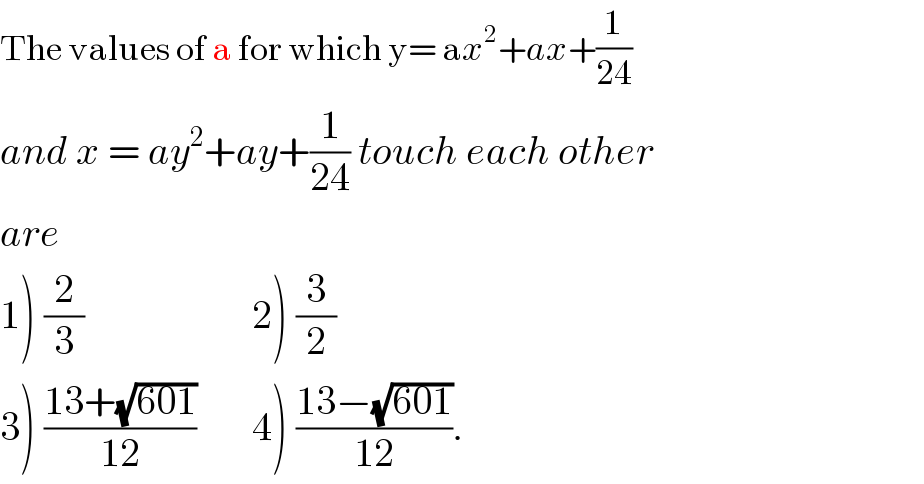
The values of a for which y= ax^2 +ax+(1/(24)) and x = ay^2 +ay+(1/(24)) touch each other are 1) (2/3) 2) (3/2) 3) ((13+(√(601)))/(12)) 4) ((13−(√(601)))/(12)).
$$\mathrm{The}\:\mathrm{values}\:\mathrm{of}\:\mathrm{a}\:\mathrm{for}\:\mathrm{which}\:\mathrm{y}=\:\mathrm{a}{x}^{\mathrm{2}} +{ax}+\frac{\mathrm{1}}{\mathrm{24}} \\ $$$${and}\:{x}\:=\:{ay}^{\mathrm{2}} +{ay}+\frac{\mathrm{1}}{\mathrm{24}}\:{touch}\:{each}\:{other} \\ $$$${are} \\ $$$$\left.\mathrm{1}\left.\right)\:\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\right)\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\left.\mathrm{3}\left.\right)\:\frac{\mathrm{13}+\sqrt{\mathrm{601}}}{\mathrm{12}}\:\:\:\:\:\:\:\mathrm{4}\right)\:\frac{\mathrm{13}−\sqrt{\mathrm{601}}}{\mathrm{12}}. \\ $$
Answered by ajfour last updated on 05/Jul/18
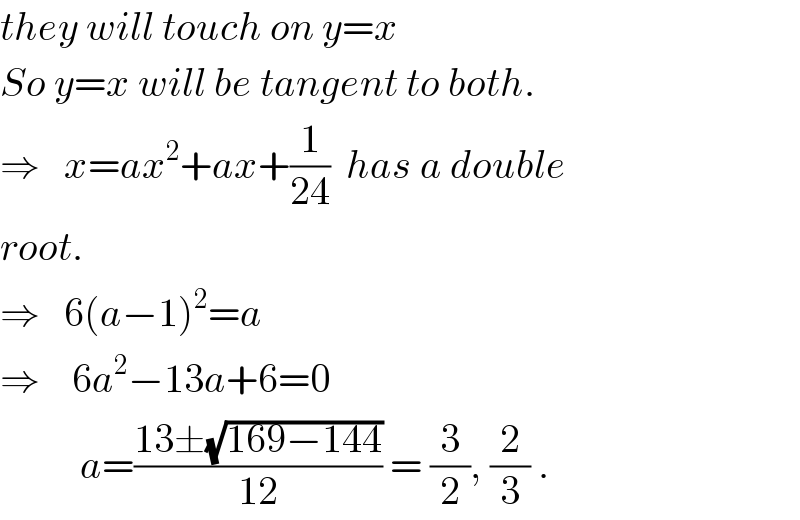
they will touch on y=x So y=x will be tangent to both. ⇒ x=ax^2 +ax+(1/(24)) has a double root. ⇒ 6(a−1)^2 =a ⇒ 6a^2 −13a+6=0 a=((13±(√(169−144)))/(12)) = (3/2), (2/3) .
$${they}\:{will}\:{touch}\:{on}\:{y}={x} \\ $$$${So}\:{y}={x}\:{will}\:{be}\:{tangent}\:{to}\:{both}. \\ $$$$\Rightarrow\:\:\:{x}={ax}^{\mathrm{2}} +{ax}+\frac{\mathrm{1}}{\mathrm{24}}\:\:{has}\:{a}\:{double} \\ $$$${root}. \\ $$$$\Rightarrow\:\:\:\mathrm{6}\left({a}−\mathrm{1}\right)^{\mathrm{2}} ={a} \\ $$$$\Rightarrow\:\:\:\:\mathrm{6}{a}^{\mathrm{2}} −\mathrm{13}{a}+\mathrm{6}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}=\frac{\mathrm{13}\pm\sqrt{\mathrm{169}−\mathrm{144}}}{\mathrm{12}}\:=\:\frac{\mathrm{3}}{\mathrm{2}},\:\frac{\mathrm{2}}{\mathrm{3}}\:. \\ $$
Commented by MJS last updated on 05/Jul/18
master you′ve been faster...
$$\mathrm{master}\:\mathrm{you}'\mathrm{ve}\:\mathrm{been}\:\mathrm{faster}… \\ $$
Commented by rahul 19 last updated on 06/Jul/18
Thank you sir!
Answered by MJS last updated on 05/Jul/18
“touching” means only 1 intersection point f(x)=ax^2 +ax+(1/(24)) f^(−1) (x): x=ay^2 +ay+(1/(24)) so they must have the common tangent y=x ax^2 +(a−1)x+(1/(24))=0 must have exactly 1 solution ⇒ ⇒ B^2 −4AC=0 ⇒ (a−1)^2 −(1/6)a=0 a^2 −((13)/6)a+1=0 o=((13)/(12))±(5/(12)) a_1 =(2/3); a_2 =(3/2)
$$“\mathrm{touching}''\:\mathrm{means}\:\mathrm{only}\:\mathrm{1}\:\mathrm{intersection}\:\mathrm{point} \\ $$$${f}\left({x}\right)={ax}^{\mathrm{2}} +{ax}+\frac{\mathrm{1}}{\mathrm{24}} \\ $$$${f}^{−\mathrm{1}} \left({x}\right):\:{x}={ay}^{\mathrm{2}} +{ay}+\frac{\mathrm{1}}{\mathrm{24}} \\ $$$$\mathrm{so}\:\mathrm{they}\:\mathrm{must}\:\mathrm{have}\:\mathrm{the}\:\mathrm{common}\:\mathrm{tangent}\:{y}={x} \\ $$$${ax}^{\mathrm{2}} +\left({a}−\mathrm{1}\right){x}+\frac{\mathrm{1}}{\mathrm{24}}=\mathrm{0}\:\mathrm{must}\:\mathrm{have}\:\mathrm{exactly}\:\mathrm{1}\:\mathrm{solution}\:\Rightarrow \\ $$$$\Rightarrow\:{B}^{\mathrm{2}} −\mathrm{4}{AC}=\mathrm{0}\:\Rightarrow\:\left({a}−\mathrm{1}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{6}}{a}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} −\frac{\mathrm{13}}{\mathrm{6}}{a}+\mathrm{1}=\mathrm{0} \\ $$$${o}=\frac{\mathrm{13}}{\mathrm{12}}\pm\frac{\mathrm{5}}{\mathrm{12}} \\ $$$${a}_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}};\:{a}_{\mathrm{2}} =\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by rahul 19 last updated on 06/Jul/18
Thank you sir!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *