Menu Close

if-cos-A-3-5-and-tan-B-12-5-where-A-and-B-are-reflex-angles-find-without-using-tables-the-value-of-a-sin-A-B-b-tan-A-B-c-cos-A-B-

Tinku Tara 0 Comments
Pin




Question Number 39588 by Rio Mike last updated on 08/Jul/18
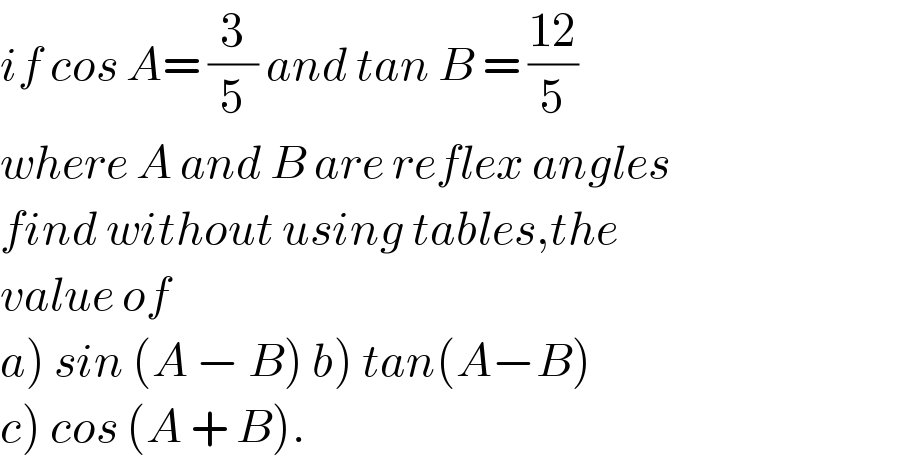
if cos A= (3/5) and tan B = ((12)/5) where A and B are reflex angles find without using tables,the value of a) sin (A − B) b) tan(A−B) c) cos (A + B).
$${if}\:{cos}\:{A}=\:\frac{\mathrm{3}}{\mathrm{5}}\:{and}\:{tan}\:{B}\:=\:\frac{\mathrm{12}}{\mathrm{5}} \\ $$$${where}\:{A}\:{and}\:{B}\:{are}\:{reflex}\:{angles} \\ $$$${find}\:{without}\:{using}\:{tables},{the} \\ $$$${value}\:{of} \\ $$$$\left.{a}\left.\right)\:{sin}\:\left({A}\:−\:{B}\right)\:{b}\right)\:{tan}\left({A}−{B}\right) \\ $$$$\left.{c}\right)\:{cos}\:\left({A}\:+\:{B}\right). \\ $$
Answered by MJS last updated on 08/Jul/18
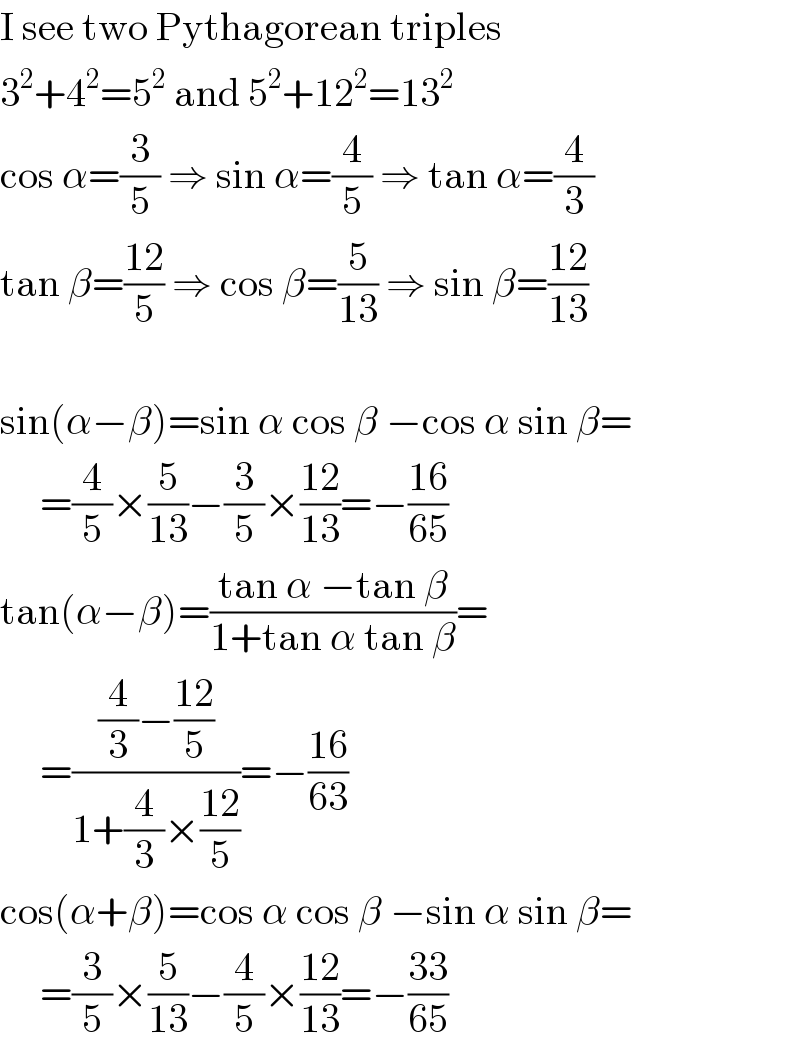
I see two Pythagorean triples 3^2 +4^2 =5^2 and 5^2 +12^2 =13^2 cos α=(3/5) ⇒ sin α=(4/5) ⇒ tan α=(4/3) tan β=((12)/5) ⇒ cos β=(5/(13)) ⇒ sin β=((12)/(13)) sin(α−β)=sin α cos β −cos α sin β= =(4/5)×(5/(13))−(3/5)×((12)/(13))=−((16)/(65)) tan(α−β)=((tan α −tan β)/(1+tan α tan β))= =(((4/3)−((12)/5))/(1+(4/3)×((12)/5)))=−((16)/(63)) cos(α+β)=cos α cos β −sin α sin β= =(3/5)×(5/(13))−(4/5)×((12)/(13))=−((33)/(65))
$$\mathrm{I}\:\mathrm{see}\:\mathrm{two}\:\mathrm{Pythagorean}\:\mathrm{triples} \\ $$$$\mathrm{3}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{5}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} =\mathrm{13}^{\mathrm{2}} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{3}}{\mathrm{5}}\:\Rightarrow\:\mathrm{sin}\:\alpha=\frac{\mathrm{4}}{\mathrm{5}}\:\Rightarrow\:\mathrm{tan}\:\alpha=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{12}}{\mathrm{5}}\:\Rightarrow\:\mathrm{cos}\:\beta=\frac{\mathrm{5}}{\mathrm{13}}\:\Rightarrow\:\mathrm{sin}\:\beta=\frac{\mathrm{12}}{\mathrm{13}} \\ $$$$ \\ $$$$\mathrm{sin}\left(\alpha−\beta\right)=\mathrm{sin}\:\alpha\:\mathrm{cos}\:\beta\:−\mathrm{cos}\:\alpha\:\mathrm{sin}\:\beta= \\ $$$$\:\:\:\:\:=\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{5}}{\mathrm{13}}−\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{12}}{\mathrm{13}}=−\frac{\mathrm{16}}{\mathrm{65}} \\ $$$$\mathrm{tan}\left(\alpha−\beta\right)=\frac{\mathrm{tan}\:\alpha\:−\mathrm{tan}\:\beta}{\mathrm{1}+\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta}= \\ $$$$\:\:\:\:\:=\frac{\frac{\mathrm{4}}{\mathrm{3}}−\frac{\mathrm{12}}{\mathrm{5}}}{\mathrm{1}+\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{12}}{\mathrm{5}}}=−\frac{\mathrm{16}}{\mathrm{63}} \\ $$$$\mathrm{cos}\left(\alpha+\beta\right)=\mathrm{cos}\:\alpha\:\mathrm{cos}\:\beta\:−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta= \\ $$$$\:\:\:\:\:=\frac{\mathrm{3}}{\mathrm{5}}×\frac{\mathrm{5}}{\mathrm{13}}−\frac{\mathrm{4}}{\mathrm{5}}×\frac{\mathrm{12}}{\mathrm{13}}=−\frac{\mathrm{33}}{\mathrm{65}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *