Menu Close

Solve-x-y-3-i-x-y-5-ii-

Tinku Tara 0 Comments
Pin




Question Number 170754 by Tawa11 last updated on 30/May/22
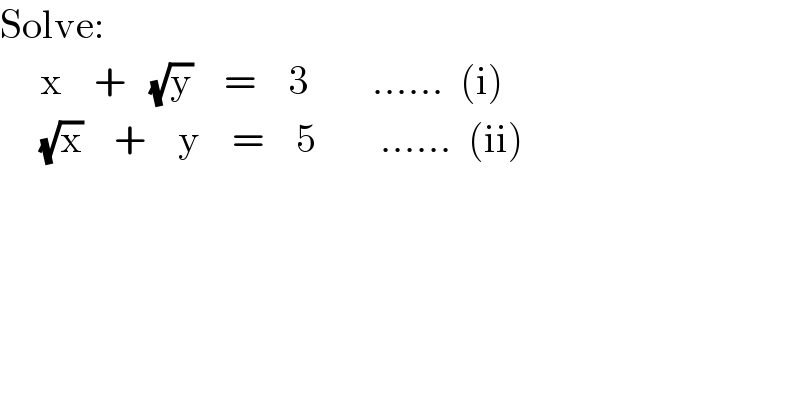
Solve: x + (√y) = 3 ...... (i) (√x) + y = 5 ...... (ii)
$$\mathrm{Solve}: \\ $$$$\:\:\:\:\:\mathrm{x}\:\:\:\:+\:\:\:\sqrt{\mathrm{y}}\:\:\:\:=\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:……\:\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\sqrt{\mathrm{x}}\:\:\:\:+\:\:\:\:\mathrm{y}\:\:\:\:=\:\:\:\:\mathrm{5}\:\:\:\:\:\:\:\:……\:\:\left(\mathrm{ii}\right) \\ $$
Commented by MJS_new last updated on 30/May/22
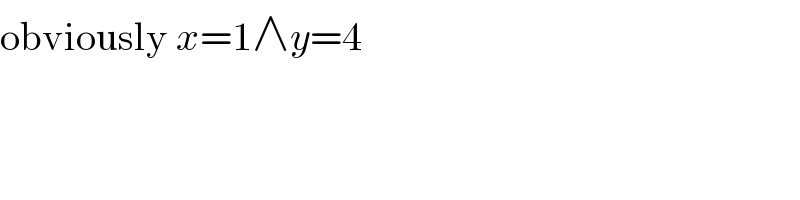
obviously x=1∧y=4
$$\mathrm{obviously}\:{x}=\mathrm{1}\wedge{y}=\mathrm{4} \\ $$
Commented by aleks041103 last updated on 30/May/22
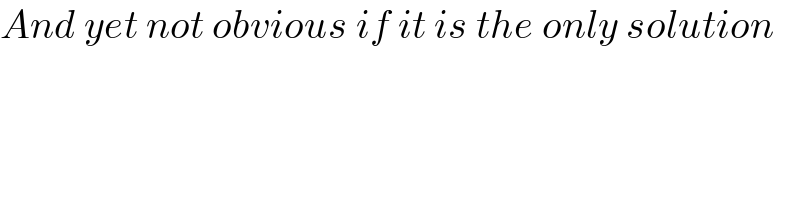
And yet not obvious if it is the only solution
$${And}\:{yet}\:{not}\:{obvious}\:{if}\:{it}\:{is}\:{the}\:{only}\:{solution} \\ $$
Commented by MJS_new last updated on 30/May/22
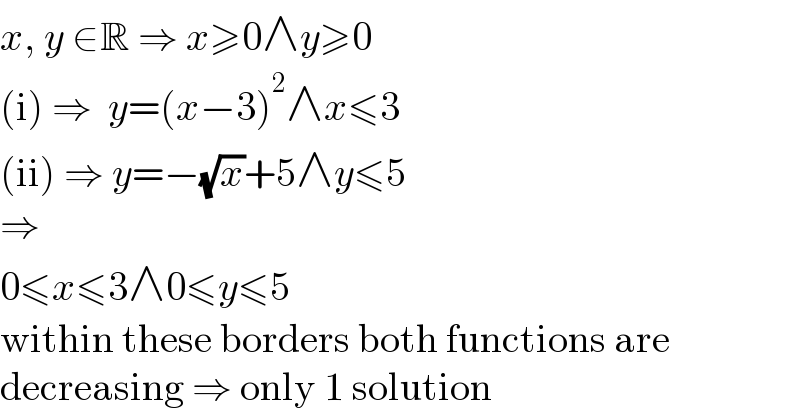
x, y ∈R ⇒ x≥0∧y≥0 (i) ⇒ y=(x−3)^2 ∧x≤3 (ii) ⇒ y=−(√x)+5∧y≤5 ⇒ 0≤x≤3∧0≤y≤5 within these borders both functions are decreasing ⇒ only 1 solution
$${x},\:{y}\:\in\mathbb{R}\:\Rightarrow\:{x}\geqslant\mathrm{0}\wedge{y}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{i}\right)\:\Rightarrow\:\:{y}=\left({x}−\mathrm{3}\right)^{\mathrm{2}} \wedge{x}\leqslant\mathrm{3} \\ $$$$\left(\mathrm{ii}\right)\:\Rightarrow\:{y}=−\sqrt{{x}}+\mathrm{5}\wedge{y}\leqslant\mathrm{5} \\ $$$$\Rightarrow \\ $$$$\mathrm{0}\leqslant{x}\leqslant\mathrm{3}\wedge\mathrm{0}\leqslant{y}\leqslant\mathrm{5} \\ $$$$\mathrm{within}\:\mathrm{these}\:\mathrm{borders}\:\mathrm{both}\:\mathrm{functions}\:\mathrm{are} \\ $$$$\mathrm{decreasing}\:\Rightarrow\:\mathrm{only}\:\mathrm{1}\:\mathrm{solution} \\ $$
Commented by aleks041103 last updated on 30/May/22
That is not necearily true. The simplest contrapoint I can think of is the case of the functions y=(1/x) and y=(5/2)−x. both are decreasing for x>0, but but there are two solutions x=(1/2) and x=2
$${That}\:{is}\:{not}\:{necearily}\:{true}. \\ $$$${The}\:{simplest}\:{contrapoint}\:{I}\:{can}\:{think}\:{of} \\ $$$${is}\:{the}\:{case}\:{of}\:{the}\:{functions} \\ $$$${y}=\frac{\mathrm{1}}{{x}}\:{and}\:{y}=\frac{\mathrm{5}}{\mathrm{2}}−{x}. \\ $$$${both}\:{are}\:{decreasing}\:{for}\:{x}>\mathrm{0},\:{but} \\ $$$${but}\:{there}\:{are}\:{two}\:{solutions} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{x}=\mathrm{2} \\ $$
Commented by Tawa11 last updated on 30/May/22
I appreciate sir
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$
Answered by aleks041103 last updated on 30/May/22
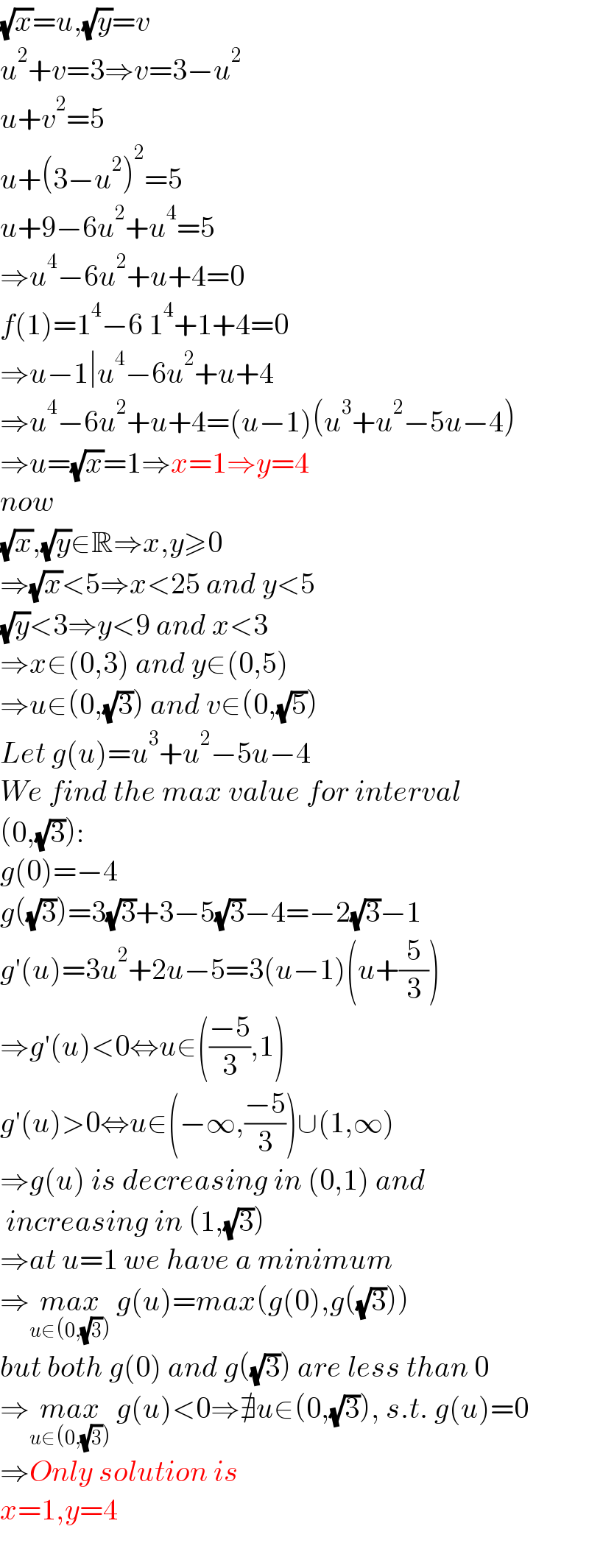
(√x)=u,(√y)=v u^2 +v=3⇒v=3−u^2 u+v^2 =5 u+(3−u^2 )^2 =5 u+9−6u^2 +u^4 =5 ⇒u^4 −6u^2 +u+4=0 f(1)=1^4 −6 1^4 +1+4=0 ⇒u−1∣u^4 −6u^2 +u+4 ⇒u^4 −6u^2 +u+4=(u−1)(u^3 +u^2 −5u−4) ⇒u=(√x)=1⇒x=1⇒y=4 now (√x),(√y)∈R⇒x,y≥0 ⇒(√x)<5⇒x<25 and y<5 (√y)<3⇒y<9 and x<3 ⇒x∈(0,3) and y∈(0,5) ⇒u∈(0,(√3)) and v∈(0,(√5)) Let g(u)=u^3 +u^2 −5u−4 We find the max value for interval (0,(√3)): g(0)=−4 g((√3))=3(√3)+3−5(√3)−4=−2(√3)−1 g′(u)=3u^2 +2u−5=3(u−1)(u+(5/3)) ⇒g′(u)<0⇔u∈(((−5)/3),1) g′(u)>0⇔u∈(−∞,((−5)/3))∪(1,∞) ⇒g(u) is decreasing in (0,1) and increasing in (1,(√3)) ⇒at u=1 we have a minimum ⇒max_(u∈(0,(√3))) g(u)=max(g(0),g((√3))) but both g(0) and g((√3)) are less than 0 ⇒max_(u∈(0,(√3))) g(u)<0⇒∄u∈(0,(√3)), s.t. g(u)=0 ⇒Only solution is x=1,y=4
$$\sqrt{{x}}={u},\sqrt{{y}}={v} \\ $$$${u}^{\mathrm{2}} +{v}=\mathrm{3}\Rightarrow{v}=\mathrm{3}−{u}^{\mathrm{2}} \\ $$$${u}+{v}^{\mathrm{2}} =\mathrm{5} \\ $$$${u}+\left(\mathrm{3}−{u}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{5} \\ $$$${u}+\mathrm{9}−\mathrm{6}{u}^{\mathrm{2}} +{u}^{\mathrm{4}} =\mathrm{5} \\ $$$$\Rightarrow{u}^{\mathrm{4}} −\mathrm{6}{u}^{\mathrm{2}} +{u}+\mathrm{4}=\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}^{\mathrm{4}} −\mathrm{6}\:\mathrm{1}^{\mathrm{4}} +\mathrm{1}+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{u}−\mathrm{1}\mid{u}^{\mathrm{4}} −\mathrm{6}{u}^{\mathrm{2}} +{u}+\mathrm{4} \\ $$$$\Rightarrow{u}^{\mathrm{4}} −\mathrm{6}{u}^{\mathrm{2}} +{u}+\mathrm{4}=\left({u}−\mathrm{1}\right)\left({u}^{\mathrm{3}} +{u}^{\mathrm{2}} −\mathrm{5}{u}−\mathrm{4}\right) \\ $$$$\Rightarrow{u}=\sqrt{{x}}=\mathrm{1}\Rightarrow{x}=\mathrm{1}\Rightarrow{y}=\mathrm{4} \\ $$$${now} \\ $$$$\sqrt{{x}},\sqrt{{y}}\in\mathbb{R}\Rightarrow{x},{y}\geqslant\mathrm{0} \\ $$$$\Rightarrow\sqrt{{x}}<\mathrm{5}\Rightarrow{x}<\mathrm{25}\:{and}\:{y}<\mathrm{5} \\ $$$$\sqrt{{y}}<\mathrm{3}\Rightarrow{y}<\mathrm{9}\:{and}\:{x}<\mathrm{3} \\ $$$$\Rightarrow{x}\in\left(\mathrm{0},\mathrm{3}\right)\:{and}\:{y}\in\left(\mathrm{0},\mathrm{5}\right) \\ $$$$\Rightarrow{u}\in\left(\mathrm{0},\sqrt{\mathrm{3}}\right)\:{and}\:{v}\in\left(\mathrm{0},\sqrt{\mathrm{5}}\right) \\ $$$${Let}\:{g}\left({u}\right)={u}^{\mathrm{3}} +{u}^{\mathrm{2}} −\mathrm{5}{u}−\mathrm{4} \\ $$$${We}\:{find}\:{the}\:{max}\:{value}\:{for}\:{interval} \\ $$$$\left(\mathrm{0},\sqrt{\mathrm{3}}\right): \\ $$$${g}\left(\mathrm{0}\right)=−\mathrm{4} \\ $$$${g}\left(\sqrt{\mathrm{3}}\right)=\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{3}−\mathrm{5}\sqrt{\mathrm{3}}−\mathrm{4}=−\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{1} \\ $$$${g}'\left({u}\right)=\mathrm{3}{u}^{\mathrm{2}} +\mathrm{2}{u}−\mathrm{5}=\mathrm{3}\left({u}−\mathrm{1}\right)\left({u}+\frac{\mathrm{5}}{\mathrm{3}}\right) \\ $$$$\Rightarrow{g}'\left({u}\right)<\mathrm{0}\Leftrightarrow{u}\in\left(\frac{−\mathrm{5}}{\mathrm{3}},\mathrm{1}\right) \\ $$$${g}'\left({u}\right)>\mathrm{0}\Leftrightarrow{u}\in\left(−\infty,\frac{−\mathrm{5}}{\mathrm{3}}\right)\cup\left(\mathrm{1},\infty\right) \\ $$$$\Rightarrow{g}\left({u}\right)\:{is}\:{decreasing}\:{in}\:\left(\mathrm{0},\mathrm{1}\right)\:{and} \\ $$$$\:{increasing}\:{in}\:\left(\mathrm{1},\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow{at}\:{u}=\mathrm{1}\:{we}\:{have}\:{a}\:{minimum} \\ $$$$\Rightarrow\underset{{u}\in\left(\mathrm{0},\sqrt{\mathrm{3}}\right)} {{max}}\:{g}\left({u}\right)={max}\left({g}\left(\mathrm{0}\right),{g}\left(\sqrt{\mathrm{3}}\right)\right) \\ $$$${but}\:{both}\:{g}\left(\mathrm{0}\right)\:{and}\:{g}\left(\sqrt{\mathrm{3}}\right)\:{are}\:{less}\:{than}\:\mathrm{0} \\ $$$$\Rightarrow\underset{{u}\in\left(\mathrm{0},\sqrt{\mathrm{3}}\right)} {{max}}\:{g}\left({u}\right)<\mathrm{0}\Rightarrow\nexists{u}\in\left(\mathrm{0},\sqrt{\mathrm{3}}\right),\:{s}.{t}.\:{g}\left({u}\right)=\mathrm{0} \\ $$$$\Rightarrow{Only}\:{solution}\:{is} \\ $$$${x}=\mathrm{1},{y}=\mathrm{4} \\ $$$$ \\ $$
Commented by Tawa11 last updated on 30/May/22
I appreciate sir
$$\mathrm{I}\:\mathrm{appreciate}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *