Question Number 39708 by NECx last updated on 10/Jul/18
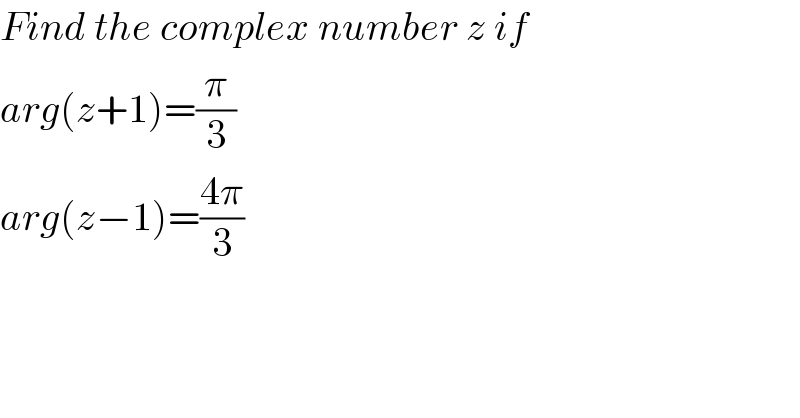
$${Find}\:{the}\:{complex}\:{number}\:{z}\:{if} \\ $$$${arg}\left({z}+\mathrm{1}\right)=\frac{\pi}{\mathrm{3}} \\ $$$${arg}\left({z}−\mathrm{1}\right)=\frac{\mathrm{4}\pi}{\mathrm{3}} \\ $$
Answered by MrW3 last updated on 10/Jul/18
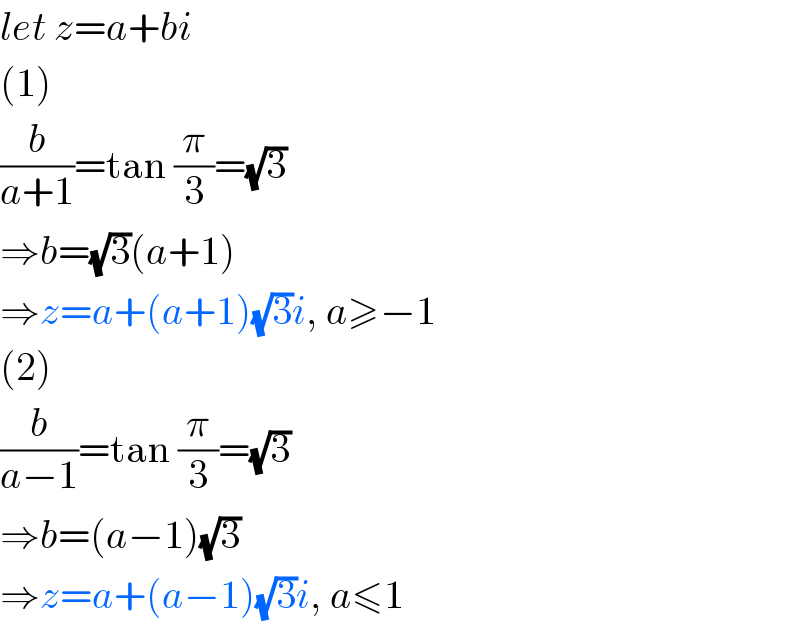
$${let}\:{z}={a}+{bi} \\ $$$$\left(\mathrm{1}\right) \\ $$$$\frac{{b}}{{a}+\mathrm{1}}=\mathrm{tan}\:\frac{\pi}{\mathrm{3}}=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{b}=\sqrt{\mathrm{3}}\left({a}+\mathrm{1}\right) \\ $$$$\Rightarrow{z}={a}+\left({a}+\mathrm{1}\right)\sqrt{\mathrm{3}}{i},\:{a}\geqslant−\mathrm{1} \\ $$$$\left(\mathrm{2}\right) \\ $$$$\frac{{b}}{{a}−\mathrm{1}}=\mathrm{tan}\:\frac{\pi}{\mathrm{3}}=\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{b}=\left({a}−\mathrm{1}\right)\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{z}={a}+\left({a}−\mathrm{1}\right)\sqrt{\mathrm{3}}{i},\:{a}\leqslant\mathrm{1} \\ $$
Commented by MrW3 last updated on 10/Jul/18
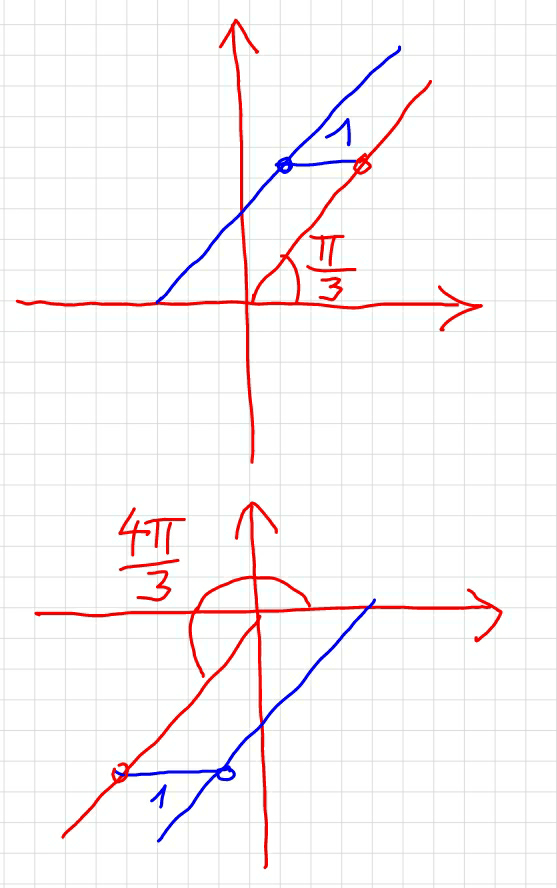
Commented by NECx last updated on 10/Jul/18
$${Thank}\:{you}\:{so}\:{much}\:{sir} \\ $$
