Question Number 39839 by math khazana by abdo last updated on 12/Jul/18
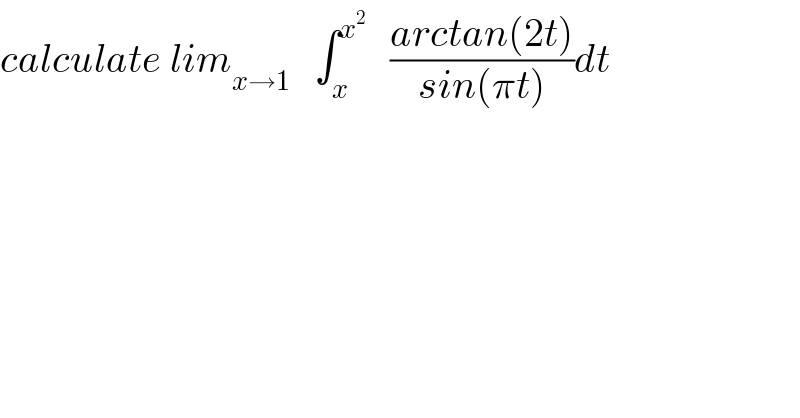
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{1}} \:\:\:\int_{{x}} ^{{x}^{\mathrm{2}} } \:\:\:\frac{{arctan}\left(\mathrm{2}{t}\right)}{{sin}\left(\pi{t}\right)}{dt} \\ $$
Commented by math khazana by abdo last updated on 30/Jul/18
![let f(x)= ∫_x ^x^2 ((arctan(2t))/(sin(πt))) dt changement t=u+1 give f(x)= ∫_(x−1) ^(x^2 −1) ((arctan(2u+2))/(sin(πu +π)))du =− ∫_(x−1) ^(x^2 −1) ((arctan(2u+2))/(sin(πu))) du but ∃c ∈]x−1,x^2 −1[/ f(x)=−arctan(2c+2) ∫_(x−1) ^(x^2 −1) (du/(sin(πu))) we have ∫_(x−1) ^(x^2 −1) (du/(sin(πu))) =_(πu =t) ∫_(π(x−1)) ^(π(x^2 −1)) (dt/(πsint)) =_(tan((t/2)) =α) (1/π) ∫_(tan((π/2)(x−1))) ^(tan((π/2)(x^2 −1))) (1/((2α)/(1+α^2 ))) ((2dα)/(1+α^2 )) =(1/π)[ln∣α∣]_(tan((π/2)(x−1))) ^(tan((π/2)(x^2 −1))) =(1/π)ln∣((tan((π/2)(x^2 −1)))/(tan((π/2)(x−1))))∣ for x∈v(1) tan((π/2)(x^2 −1))∼(π/2)(x^2 −1) and tan((π/2)(x−1))∼ (π/2)(x−1) ⇒∣((tan(...))/(tan(..)))∣∼∣x+1∣⇒ lim_(x→1) ∫_(x−1) ^(x^2 −1) (du/(sin(πu))) =((ln(2))/π) ⇒ lim_(x→1) f(x)=−arctan(2)((ln(2))/π) .](https://www.tinkutara.com/question/Q40947.png)
$${let}\:{f}\left({x}\right)=\:\int_{{x}} ^{{x}^{\mathrm{2}} } \:\:\:\frac{{arctan}\left(\mathrm{2}{t}\right)}{{sin}\left(\pi{t}\right)}\:{dt}\:{changement}\:{t}={u}+\mathrm{1} \\ $$$${give}\:{f}\left({x}\right)=\:\int_{{x}−\mathrm{1}} ^{{x}^{\mathrm{2}} −\mathrm{1}} \:\:\frac{{arctan}\left(\mathrm{2}{u}+\mathrm{2}\right)}{{sin}\left(\pi{u}\:+\pi\right)}{du} \\ $$$$\left.=−\:\int_{{x}−\mathrm{1}} ^{{x}^{\mathrm{2}} −\mathrm{1}} \:\:\:\frac{{arctan}\left(\mathrm{2}{u}+\mathrm{2}\right)}{{sin}\left(\pi{u}\right)}\:{du}\:{but}\:\exists{c}\:\in\right]{x}−\mathrm{1},{x}^{\mathrm{2}} −\mathrm{1}\left[/\right. \\ $$$${f}\left({x}\right)=−{arctan}\left(\mathrm{2}{c}+\mathrm{2}\right)\:\int_{{x}−\mathrm{1}} ^{{x}^{\mathrm{2}} \:−\mathrm{1}} \:\:\:\frac{{du}}{{sin}\left(\pi{u}\right)}\:{we}\:{have} \\ $$$$\int_{{x}−\mathrm{1}} ^{{x}^{\mathrm{2}} −\mathrm{1}} \:\:\frac{{du}}{{sin}\left(\pi{u}\right)}\:=_{\pi{u}\:={t}} \:\:\:\int_{\pi\left({x}−\mathrm{1}\right)} ^{\pi\left({x}^{\mathrm{2}} −\mathrm{1}\right)} \:\:\frac{{dt}}{\pi{sint}} \\ $$$$=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)\:=\alpha} \:\:\:\:\frac{\mathrm{1}}{\pi}\:\int_{{tan}\left(\frac{\pi}{\mathrm{2}}\left({x}−\mathrm{1}\right)\right)} ^{{tan}\left(\frac{\pi}{\mathrm{2}}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\right)} \:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{2}\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} }}\:\frac{\mathrm{2}{d}\alpha}{\mathrm{1}+\alpha^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\pi}\left[{ln}\mid\alpha\mid\right]_{{tan}\left(\frac{\pi}{\mathrm{2}}\left({x}−\mathrm{1}\right)\right)} ^{{tan}\left(\frac{\pi}{\mathrm{2}}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\right)} \:\:=\frac{\mathrm{1}}{\pi}{ln}\mid\frac{{tan}\left(\frac{\pi}{\mathrm{2}}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\right)}{{tan}\left(\frac{\pi}{\mathrm{2}}\left({x}−\mathrm{1}\right)\right)}\mid \\ $$$${for}\:{x}\in{v}\left(\mathrm{1}\right)\:{tan}\left(\frac{\pi}{\mathrm{2}}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\right)\sim\frac{\pi}{\mathrm{2}}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\:{and} \\ $$$${tan}\left(\frac{\pi}{\mathrm{2}}\left({x}−\mathrm{1}\right)\right)\sim\:\frac{\pi}{\mathrm{2}}\left({x}−\mathrm{1}\right)\:\Rightarrow\mid\frac{{tan}\left(…\right)}{{tan}\left(..\right)}\mid\sim\mid{x}+\mathrm{1}\mid\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} \:\int_{{x}−\mathrm{1}} ^{{x}^{\mathrm{2}} −\mathrm{1}} \:\:\:\frac{{du}}{{sin}\left(\pi{u}\right)}\:=\frac{{ln}\left(\mathrm{2}\right)}{\pi}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} {f}\left({x}\right)=−{arctan}\left(\mathrm{2}\right)\frac{{ln}\left(\mathrm{2}\right)}{\pi}\:. \\ $$$$ \\ $$$$ \\ $$
