lim-n-k-1-n-1-k-2-n-

Question Number 105498 by Dwaipayan Shikari last updated on 29/Jul/20

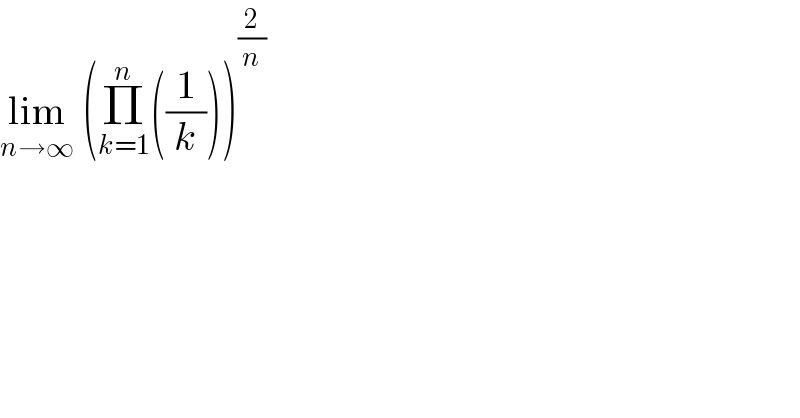
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\frac{\mathrm{1}}{{k}}\right)\right)^{\frac{\mathrm{2}}{{n}}} \\ $$

Commented by JDamian last updated on 29/Jul/20

"From n=1 up to n"? -- Please, review your question

Commented by Ar Brandon last updated on 29/Jul/20

You mean lim_(n→∞) [Π_(k=1) ^n ((1/k))]^(2/n) , lim_(n→∞) [Π_(k=1) ^n ((1/n))]^(2/k) , lim_(n→∞) [Π_(k=1) ^n ((1/k))]^(2/k) Or that′s just how it is ? I felt it should be otherwise.

$$\mathrm{You}\:\mathrm{mean}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\frac{\mathrm{1}}{\mathrm{k}}\right)\right]^{\frac{\mathrm{2}}{\mathrm{n}}} ,\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right]^{\frac{\mathrm{2}}{\mathrm{k}}} ,\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left[\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\frac{\mathrm{1}}{\mathrm{k}}\right)\right]^{\frac{\mathrm{2}}{\mathrm{k}}} \\ $$$$\mathrm{Or}\:\mathrm{that}'\mathrm{s}\:\mathrm{just}\:\mathrm{how}\:\mathrm{it}\:\mathrm{is}\:?\:\mathrm{I}\:\mathrm{felt}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{otherwise}. \\ $$

Commented by Dwaipayan Shikari last updated on 29/Jul/20

$${The}\:{first}\:{one} \\ $$

Answered by mathmax by abdo last updated on 29/Jul/20

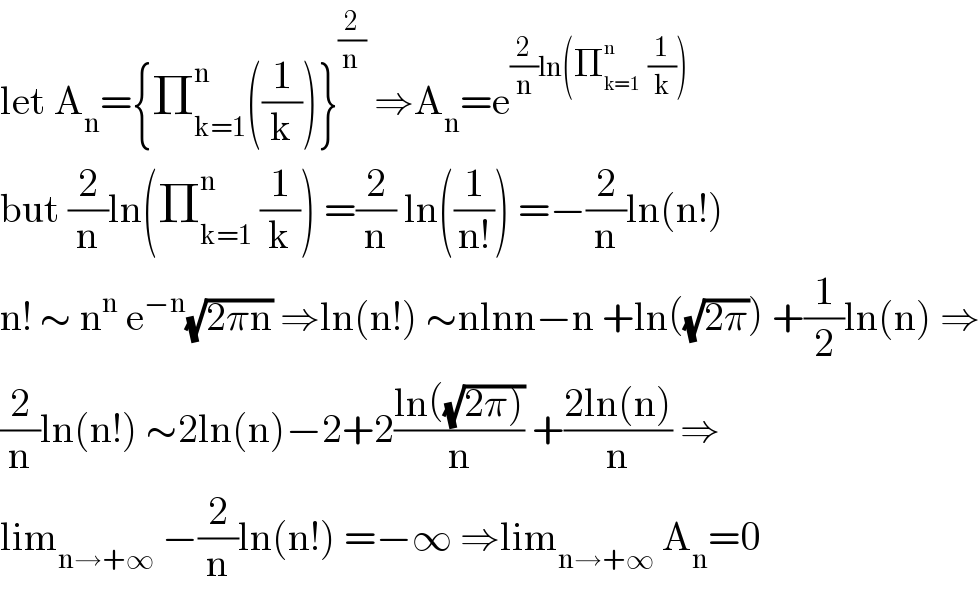
let A_n ={Π_(k=1) ^n ((1/k))}^(2/(n )) ⇒A_n =e^((2/n)ln(Π_(k=1) ^n (1/k))) but (2/n)ln(Π_(k=1) ^n (1/k)) =(2/n) ln((1/(n!))) =−(2/n)ln(n!) n! ∼ n^n e^(−n) (√(2πn)) ⇒ln(n!) ∼nlnn−n +ln((√(2π))) +(1/2)ln(n) ⇒ (2/n)ln(n!) ∼2ln(n)−2+2((ln((√(2π))))/n) +((2ln(n))/n) ⇒ lim_(n→+∞) −(2/n)ln(n!) =−∞ ⇒lim_(n→+∞) A_n =0

$$\mathrm{let}\:\mathrm{A}_{\mathrm{n}} =\left\{\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{k}}\right)\right\}^{\frac{\mathrm{2}}{\mathrm{n}\:}} \:\Rightarrow\mathrm{A}_{\mathrm{n}} =\mathrm{e}^{\frac{\mathrm{2}}{\mathrm{n}}\mathrm{ln}\left(\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\:\frac{\mathrm{1}}{\mathrm{k}}\right)} \\ $$$$\mathrm{but}\:\frac{\mathrm{2}}{\mathrm{n}}\mathrm{ln}\left(\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}\right)\:=\frac{\mathrm{2}}{\mathrm{n}}\:\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{n}!}\right)\:=−\frac{\mathrm{2}}{\mathrm{n}}\mathrm{ln}\left(\mathrm{n}!\right) \\ $$$$\mathrm{n}!\:\sim\:\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\:\Rightarrow\mathrm{ln}\left(\mathrm{n}!\right)\:\sim\mathrm{nlnn}−\mathrm{n}\:+\mathrm{ln}\left(\sqrt{\mathrm{2}\pi}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{n}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{2}}{\mathrm{n}}\mathrm{ln}\left(\mathrm{n}!\right)\:\sim\mathrm{2ln}\left(\mathrm{n}\right)−\mathrm{2}+\mathrm{2}\frac{\mathrm{ln}\left(\sqrt{\left.\mathrm{2}\pi\right)}\right.}{\mathrm{n}}\:+\frac{\mathrm{2ln}\left(\mathrm{n}\right)}{\mathrm{n}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:−\frac{\mathrm{2}}{\mathrm{n}}\mathrm{ln}\left(\mathrm{n}!\right)\:=−\infty\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\mathrm{0} \\ $$

Commented by Dwaipayan Shikari last updated on 29/Jul/20

$${Thanking}\:{you} \\ $$

Commented by Ar Brandon last updated on 29/Jul/20

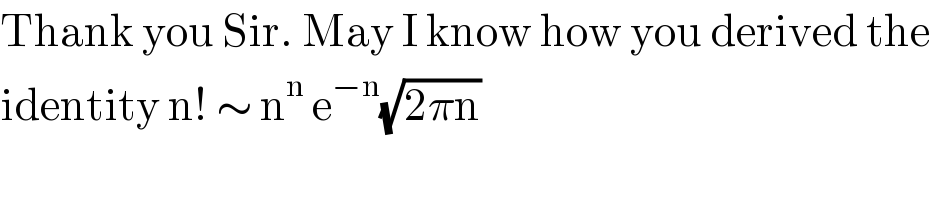
Thank you Sir. May I know how you derived the identity n! ∼ n^n e^(−n) (√(2πn))

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}.\:\mathrm{May}\:\mathrm{I}\:\mathrm{know}\:\mathrm{how}\:\mathrm{you}\:\mathrm{derived}\:\mathrm{the} \\ $$$$\mathrm{identity}\:\mathrm{n}!\:\sim\:\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\: \\ $$

Commented by PRITHWISH SEN 2 last updated on 29/Jul/20

starling approximation for higher value of n

$$\mathrm{starling}\:\mathrm{approximation}\:\mathrm{for}\:\mathrm{higher}\:\mathrm{value}\:\mathrm{of}\:\mathrm{n} \\ $$

Commented by Ar Brandon last updated on 29/Jul/20

OK thanks

Commented by mathmax by abdo last updated on 30/Jul/20

sir brandon this is stirling formulae for the proot enter to internet you find a lots of methods for this...

$$\mathrm{sir}\:\mathrm{brandon}\:\mathrm{this}\:\mathrm{is}\:\mathrm{stirling}\:\mathrm{formulae}\:\mathrm{for}\:\mathrm{the}\:\mathrm{proot}\:\mathrm{enter}\:\mathrm{to} \\ $$$$\mathrm{internet}\:\mathrm{you}\:\mathrm{find}\:\mathrm{a}\:\mathrm{lots}\:\mathrm{of}\:\mathrm{methods}\:\mathrm{for}\:\mathrm{this}… \\ $$

Facebook Tweet Pin

lim-n-k-1-n-1-k-2-n-

Leave a Reply Cancel reply