Question Number 171064 by 119065 last updated on 07/Jun/22
![When A^(−1) = [(3,1),(8,4) ] find the A=? ,∣A^(−1) ∣∙A=?](https://www.tinkutara.com/question/Q171064.png)
$${When}\:\:{A}^{−\mathrm{1}} =\begin{bmatrix}{\mathrm{3}}&{\mathrm{1}}\\{\mathrm{8}}&{\mathrm{4}}\end{bmatrix} \\ $$$${find}\:{the}\:\:{A}=?\:,\mid{A}^{−\mathrm{1}} \mid\centerdot{A}=? \\ $$
Answered by som(math1967) last updated on 07/Jun/22
![Adj A^(−1) = [(4,(−8)),((−1),3) ]^T = [(4,(−1)),((−8),3) ] ∣A^(−1) ∣=12−8=4 A=(1/4) [(4,(−1)),((−8),3) ] ∣A^(−1) ∣A=4×(1/4) [(4,(−1)),((−8),3) ]= [(4,(−1)),((−8),3) ]](https://www.tinkutara.com/question/Q171075.png)
$$\:{Adj}\:{A}^{−\mathrm{1}} =\begin{bmatrix}{\mathrm{4}}&{−\mathrm{8}}\\{−\mathrm{1}}&{\mathrm{3}}\end{bmatrix}^{{T}} =\begin{bmatrix}{\mathrm{4}}&{−\mathrm{1}}\\{−\mathrm{8}}&{\mathrm{3}}\end{bmatrix} \\ $$$$\mid{A}^{−\mathrm{1}} \mid=\mathrm{12}−\mathrm{8}=\mathrm{4} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{4}}\begin{bmatrix}{\mathrm{4}}&{−\mathrm{1}}\\{−\mathrm{8}}&{\mathrm{3}}\end{bmatrix} \\ $$$$\mid{A}^{−\mathrm{1}} \mid{A}=\mathrm{4}×\frac{\mathrm{1}}{\mathrm{4}}\begin{bmatrix}{\mathrm{4}}&{−\mathrm{1}}\\{−\mathrm{8}}&{\mathrm{3}}\end{bmatrix}=\begin{bmatrix}{\mathrm{4}}&{−\mathrm{1}}\\{−\mathrm{8}}&{\mathrm{3}}\end{bmatrix} \\ $$
Commented by 119065 last updated on 07/Jun/22

$${nice}\:{solution} \\ $$
Answered by manxsol last updated on 05/Feb/23
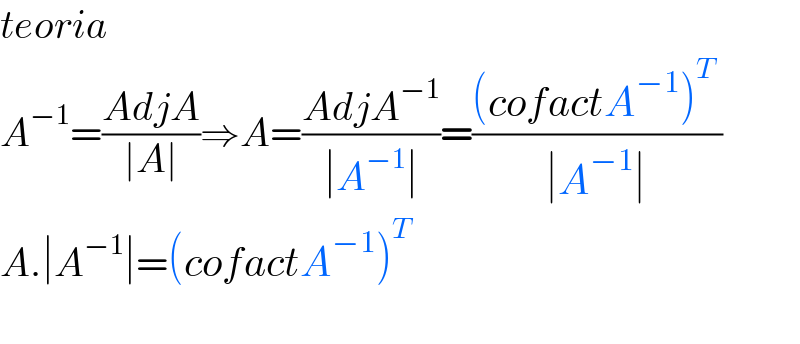
$${teoria} \\ $$$${A}^{−\mathrm{1}} =\frac{{AdjA}}{\mid{A}\mid}\Rightarrow{A}=\frac{{AdjA}^{−\mathrm{1}} }{\mid{A}^{−\mathrm{1}} \mid}=\frac{\left({cofactA}^{−\mathrm{1}} \right)^{{T}} \:}{\mid{A}^{−\mathrm{1}} \mid} \\ $$$${A}.\mid{A}^{−\mathrm{1}} \mid=\left({cofactA}^{−\mathrm{1}} \right)^{{T}} \: \\ $$$$ \\ $$
