Question Number 171160 by mokys last updated on 08/Jun/22

Answered by thfchristopher last updated on 09/Jun/22
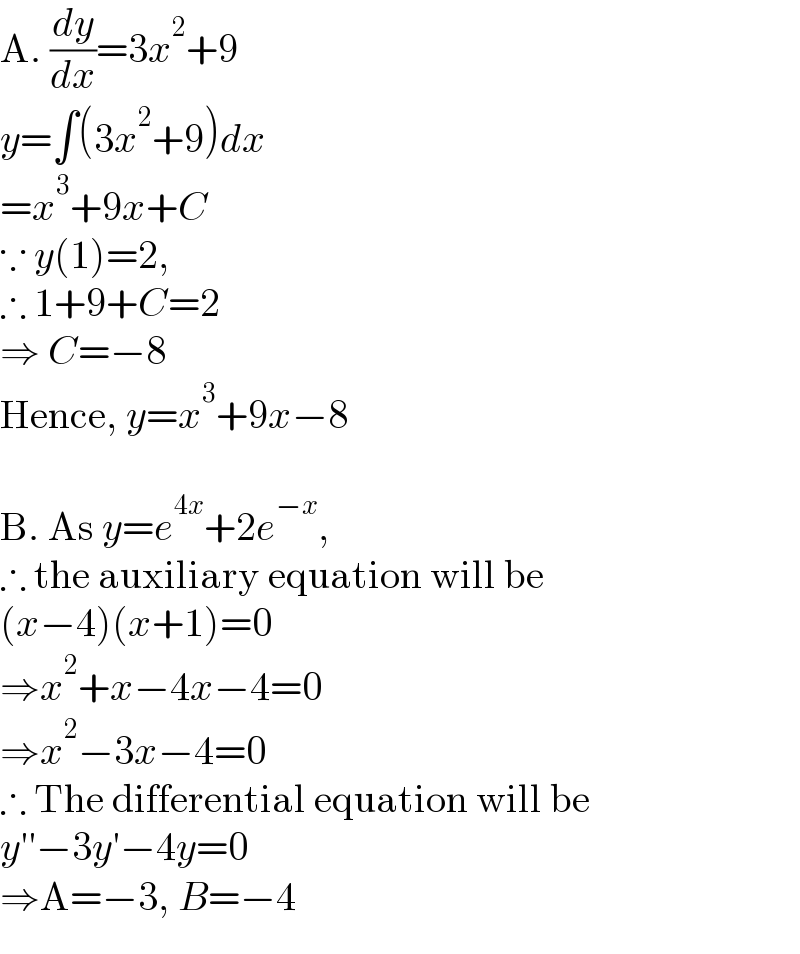
$$\mathrm{A}.\:\frac{{dy}}{{dx}}=\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9} \\ $$$${y}=\int\left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{9}\right){dx} \\ $$$$={x}^{\mathrm{3}} +\mathrm{9}{x}+{C} \\ $$$$\because\:{y}\left(\mathrm{1}\right)=\mathrm{2}, \\ $$$$\therefore\:\mathrm{1}+\mathrm{9}+{C}=\mathrm{2} \\ $$$$\Rightarrow\:{C}=−\mathrm{8} \\ $$$$\mathrm{Hence},\:{y}={x}^{\mathrm{3}} +\mathrm{9}{x}−\mathrm{8} \\ $$$$\: \\ $$$$\mathrm{B}.\:\mathrm{As}\:{y}={e}^{\mathrm{4}{x}} +\mathrm{2}{e}^{−{x}} , \\ $$$$\therefore\:\mathrm{the}\:\mathrm{auxiliary}\:\mathrm{equation}\:\mathrm{will}\:\mathrm{be} \\ $$$$\left({x}−\mathrm{4}\right)\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} +{x}−\mathrm{4}{x}−\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{3}{x}−\mathrm{4}=\mathrm{0} \\ $$$$\therefore\:\mathrm{The}\:\mathrm{differential}\:\mathrm{equation}\:\mathrm{will}\:\mathrm{be} \\ $$$${y}''−\mathrm{3}{y}'−\mathrm{4}{y}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{A}=−\mathrm{3},\:{B}=−\mathrm{4} \\ $$
