Question Number 171189 by mathlove last updated on 09/Jun/22
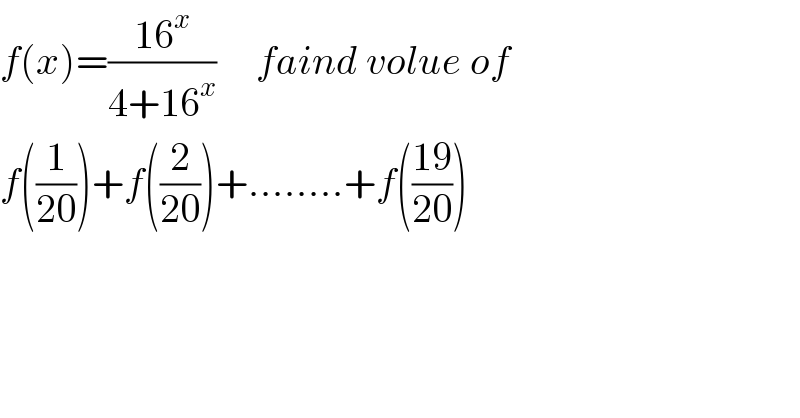
$${f}\left({x}\right)=\frac{\mathrm{16}^{{x}} }{\mathrm{4}+\mathrm{16}^{{x}} }\:\:\:\:\:{faind}\:{volue}\:{of} \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{20}}\right)+{f}\left(\frac{\mathrm{2}}{\mathrm{20}}\right)+……..+{f}\left(\frac{\mathrm{19}}{\mathrm{20}}\right) \\ $$
Answered by cortano1 last updated on 09/Jun/22
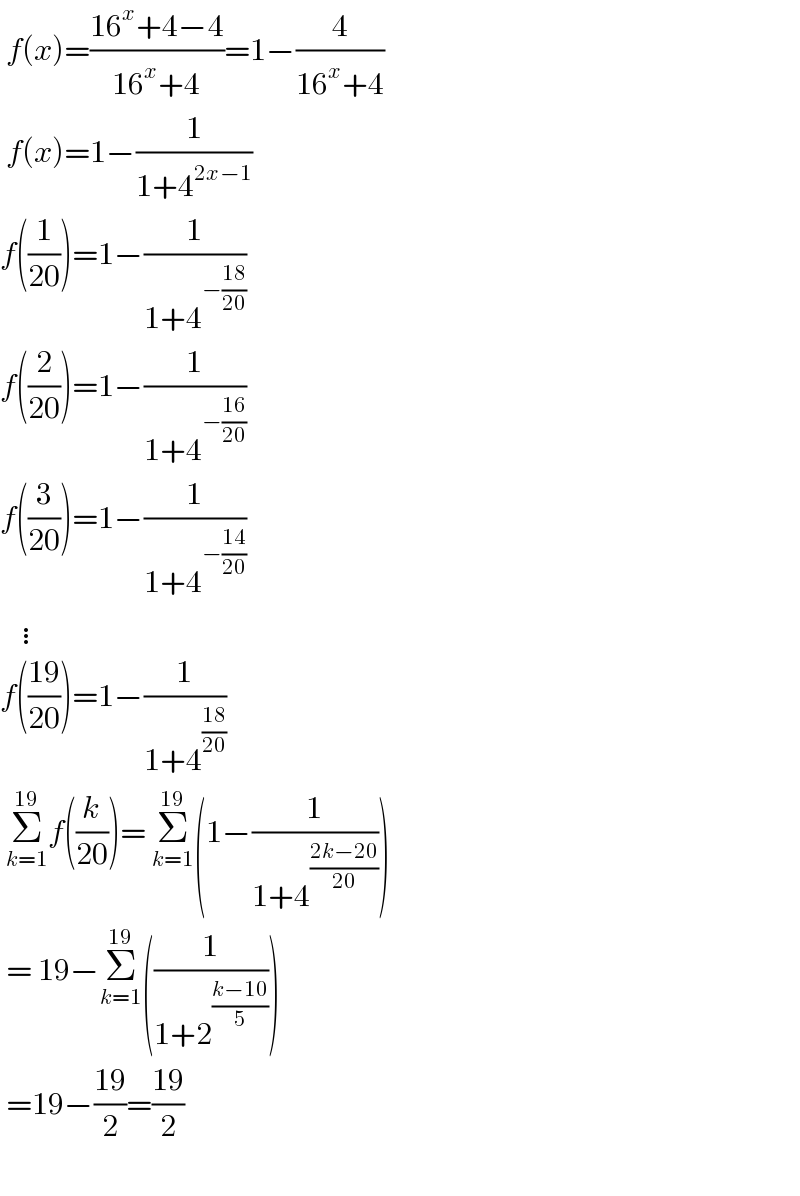
$$\:{f}\left({x}\right)=\frac{\mathrm{16}^{{x}} +\mathrm{4}−\mathrm{4}}{\mathrm{16}^{{x}} +\mathrm{4}}=\mathrm{1}−\frac{\mathrm{4}}{\mathrm{16}^{{x}} +\mathrm{4}} \\ $$$$\:{f}\left({x}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{4}^{\mathrm{2}{x}−\mathrm{1}} } \\ $$$${f}\left(\frac{\mathrm{1}}{\mathrm{20}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{4}^{−\frac{\mathrm{18}}{\mathrm{20}}} } \\ $$$${f}\left(\frac{\mathrm{2}}{\mathrm{20}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{4}^{−\frac{\mathrm{16}}{\mathrm{20}}} } \\ $$$${f}\left(\frac{\mathrm{3}}{\mathrm{20}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{4}^{−\frac{\mathrm{14}}{\mathrm{20}}} } \\ $$$$\:\:\:\vdots \\ $$$${f}\left(\frac{\mathrm{19}}{\mathrm{20}}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{4}^{\frac{\mathrm{18}}{\mathrm{20}}} } \\ $$$$\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{19}} {\sum}}{f}\left(\frac{{k}}{\mathrm{20}}\right)=\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{19}} {\sum}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{4}^{\frac{\mathrm{2}{k}−\mathrm{20}}{\mathrm{20}}} }\right) \\ $$$$\:=\:\mathrm{19}−\underset{{k}=\mathrm{1}} {\overset{\mathrm{19}} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{2}^{\frac{{k}−\mathrm{10}}{\mathrm{5}}} }\right) \\ $$$$\:=\mathrm{19}−\frac{\mathrm{19}}{\mathrm{2}}=\frac{\mathrm{19}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by mathlove last updated on 09/Jun/22

$${thanks} \\ $$
Answered by Jamshidbek last updated on 09/Jun/22
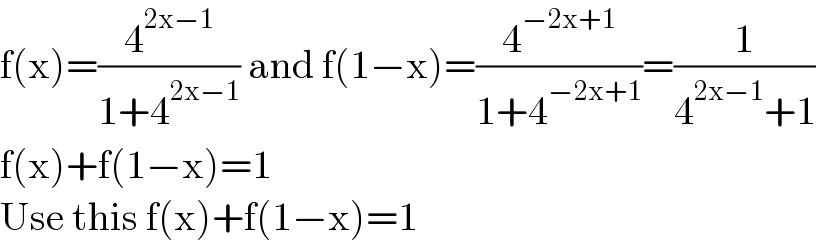
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{4}^{\mathrm{2x}−\mathrm{1}} }{\mathrm{1}+\mathrm{4}^{\mathrm{2x}−\mathrm{1}} }\:\mathrm{and}\:\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right)=\frac{\mathrm{4}^{−\mathrm{2x}+\mathrm{1}} }{\mathrm{1}+\mathrm{4}^{−\mathrm{2x}+\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2x}−\mathrm{1}} +\mathrm{1}} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right)=\mathrm{1} \\ $$$$\mathrm{Use}\:\mathrm{this}\:\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{1}−\mathrm{x}\right)=\mathrm{1} \\ $$
