Menu Close

Change-to-polar-coordinates-4a-0-y-2-4a-a-x-2-y-2-x-2-y-2-dx-dy-

Tinku Tara 0 Comments
Pin




Question Number 171260 by udaythool last updated on 11/Jun/22
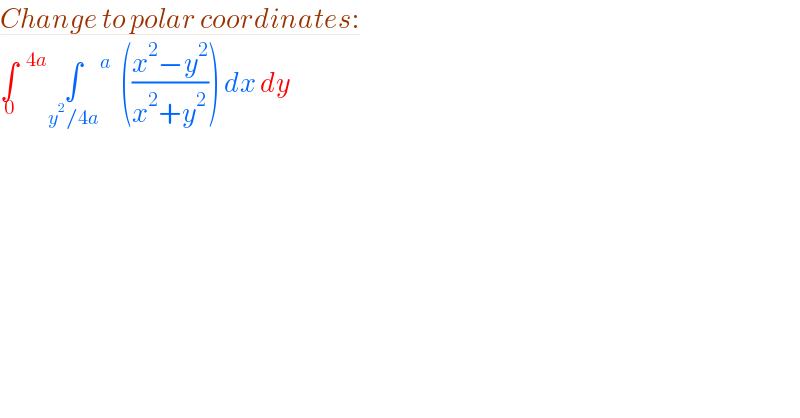
Change to polar coordinates: ∫^( 4a) _0 ∫_(y^2 /4a) ^a (((x^2 −y^2 )/(x^2 +y^2 ))) dx dy
$$\underline{{Change}\:{to}\:{polar}\:{coordinates}:} \\ $$$$\underset{\mathrm{0}} {\int}^{\:\:\mathrm{4}{a}} \underset{{y}^{\mathrm{2}} /\mathrm{4}{a}} {\int}\overset{{a}} {\:}\:\:\left(\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)\:{dx}\:{dy} \\ $$
Answered by udaythool last updated on 13/Jun/22
Solution: Let f≡ (((x^2 −y^2 )/(x^2 +y^2 )))⇒f = rcos 2θ ⇒I=∫_0 ^( 4a) ∫_(y^2 /4a) ^( a) f dxdy =∫_0 ^( 2a) ∫_(y^2 /4a) ^( a) f dxdy −∫_(2a) ^( 4a) ∫_a ^( y^2 /4a) f dxdy =∫∫_(R_1 ) − ∫∫_(R_2 ) =I_1 −I_2 where R_1 ≡0≤y≤2a, y^2 /4a≤x≤a and R_2 ≡2a≤y≤4a, a≤x≤ y^2 /4a For polar coordinates we should have to divide both R_1 into A, B and R_2 into C, D subregions by a line from origin and (a, 2a). Thus I_1 =I_A +I_B and I_2 =I_C +I_D For A, 0≤θ≤tan^(−1) 2 and 0≤r≤a/cos θ ⇒I_A =∫_0 ^(tan^(−1) 2) ∫_0 ^(a/cos θ) r cos2θ dr dθ =a^2 (tan^(−1) 2−1). For B, tan^(−1) 2≤θ≤π/2 and 0≤r≤4acos θ/sin^2 θ ⇒I_B =∫_(tan^(−1) 2) ^(π/2) ∫_0 ^(4acos θ/sin^2 θ) r cos2θ dr dθ I_B =8a^2 (π−23/24−2tan^(−1) 2). For C, π/4≤θ≤tan^(−1) 2 and 4acos θ/sin^2 θ≤r≤4a/sin θ ⇒I_C =∫_(π/4) ^(tan^(−1) 2) ∫_(4acos θ/sin^2 θ) ^(4a/sin θ) r cos2θ dr dθ I_C =8a^2 (π+29/24−4tan^(−1) 2). And for D, tan^(−1) 2≤θ≤tan^(−1) 4 and a/cos θ≤r≤4a/sin θ ⇒I_D =∫_(tan^(−1) 2) ^(tan^(−1) 4) ∫_(a/cos θ) ^(4a/sin θ) r cos2θ dr dθ I_D =a^2 (3+174tan^(−1) 2−17tan^(−1) 4). ∴ I=(((−64)/3))a^2 +17a^2 tan^(−1) 4
$$\mathrm{Solution}:\:\mathrm{Let}\:{f}\equiv\:\left(\frac{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)\Rightarrow{f}\:=\:{r}\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\Rightarrow{I}=\int_{\mathrm{0}} ^{\:\mathrm{4}{a}} \int_{{y}^{\mathrm{2}} /\mathrm{4}{a}} ^{\:\:\:\:{a}} {f}\:{dxdy}\: \\ $$$$=\int_{\mathrm{0}} ^{\:\mathrm{2}{a}} \int_{{y}^{\mathrm{2}} /\mathrm{4}{a}} ^{\:\:\:\:{a}} {f}\:{dxdy}\:−\int_{\mathrm{2}{a}} ^{\:\mathrm{4}{a}} \int_{{a}} ^{\:\:{y}^{\mathrm{2}} /\mathrm{4}{a}} {f}\:{dxdy} \\ $$$$=\underset{{R}_{\mathrm{1}} } {\int\int}\:\:−\:\underset{{R}_{\mathrm{2}} } {\int\int}\:={I}_{\mathrm{1}} −{I}_{\mathrm{2}} \\ $$$$\mathrm{where}\:{R}_{\mathrm{1}} \equiv\mathrm{0}\leq{y}\leq\mathrm{2}{a},\:{y}^{\mathrm{2}} /\mathrm{4}{a}\leq{x}\leq{a} \\ $$$$\mathrm{and}\:{R}_{\mathrm{2}} \equiv\mathrm{2}{a}\leq{y}\leq\mathrm{4}{a},\:\:\:{a}\leq{x}\leq\:{y}^{\mathrm{2}} /\mathrm{4}{a} \\ $$$$\mathrm{For}\:\mathrm{polar}\:\mathrm{coordinates}\:\mathrm{we}\:\mathrm{should}\:\mathrm{have} \\ $$$$\mathrm{to}\:\mathrm{divide}\:\mathrm{both}\:{R}_{\mathrm{1}} \:\mathrm{into}\:{A},\:{B}\:\mathrm{and}\:{R}_{\mathrm{2}} \:\mathrm{into}\:{C},\:{D} \\ $$$$\mathrm{subregions}\:\mathrm{by}\:\mathrm{a}\:\mathrm{line}\:\mathrm{from}\:\mathrm{origin}\:\mathrm{and}\:\left(\mathrm{a},\:\mathrm{2}{a}\right).\: \\ $$$$\mathrm{Thus}\:{I}_{\mathrm{1}} ={I}_{{A}} +{I}_{{B}} \:\mathrm{and}\:{I}_{\mathrm{2}} ={I}_{{C}} +{I}_{{D}} \\ $$$$\mathrm{For}\:{A},\:\mathrm{0}\leq\theta\leq\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\:\mathrm{and}\:\mathrm{0}\leq{r}\leq{a}/\mathrm{cos}\:\theta \\ $$$$\Rightarrow{I}_{{A}} =\int_{\mathrm{0}} ^{\mathrm{tan}^{−\mathrm{1}} \mathrm{2}} \int_{\mathrm{0}} ^{{a}/\mathrm{cos}\:\theta} {r}\:\mathrm{cos2}\theta\:{dr}\:{d}\theta\:={a}^{\mathrm{2}} \left(\mathrm{tan}^{−\mathrm{1}} \mathrm{2}−\mathrm{1}\right). \\ $$$$\mathrm{For}\:{B},\:\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\leq\theta\leq\pi/\mathrm{2}\:\mathrm{and}\:\mathrm{0}\leq{r}\leq\mathrm{4}{a}\mathrm{cos}\:\theta/\mathrm{sin}^{\mathrm{2}} \theta \\ $$$$\Rightarrow{I}_{{B}} =\int_{\mathrm{tan}^{−\mathrm{1}} \mathrm{2}} ^{\pi/\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{4}{a}\mathrm{cos}\:\theta/\mathrm{sin}^{\mathrm{2}} \theta} {r}\:\mathrm{cos2}\theta\:{dr}\:{d}\theta \\ $$$${I}_{{B}} =\mathrm{8}{a}^{\mathrm{2}} \left(\pi−\mathrm{23}/\mathrm{24}−\mathrm{2tan}^{−\mathrm{1}} \mathrm{2}\right). \\ $$$$\mathrm{For}\:{C},\:\pi/\mathrm{4}\leq\theta\leq\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\:\mathrm{and}\:\mathrm{4}{a}\mathrm{cos}\:\theta/\mathrm{sin}^{\mathrm{2}} \theta\leq{r}\leq\mathrm{4}{a}/\mathrm{sin}\:\theta \\ $$$$\Rightarrow{I}_{{C}} =\int_{\pi/\mathrm{4}} ^{\mathrm{tan}^{−\mathrm{1}} \mathrm{2}} \int_{\mathrm{4}{a}\mathrm{cos}\:\theta/\mathrm{sin}^{\mathrm{2}} \theta} ^{\mathrm{4}{a}/\mathrm{sin}\:\theta} {r}\:\mathrm{cos2}\theta\:{dr}\:{d}\theta \\ $$$${I}_{{C}} =\mathrm{8}{a}^{\mathrm{2}} \left(\pi+\mathrm{29}/\mathrm{24}−\mathrm{4tan}^{−\mathrm{1}} \mathrm{2}\right). \\ $$$$\mathrm{And}\:\mathrm{for}\:{D},\:\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\leq\theta\leq\mathrm{tan}^{−\mathrm{1}} \mathrm{4}\:\mathrm{and}\:{a}/\mathrm{cos}\:\theta\leq{r}\leq\mathrm{4}{a}/\mathrm{sin}\:\theta \\ $$$$\Rightarrow{I}_{{D}} =\int_{\mathrm{tan}^{−\mathrm{1}} \mathrm{2}} ^{\mathrm{tan}^{−\mathrm{1}} \mathrm{4}} \int_{{a}/\mathrm{cos}\:\theta} ^{\mathrm{4}{a}/\mathrm{sin}\:\theta} {r}\:\mathrm{cos2}\theta\:{dr}\:{d}\theta \\ $$$${I}_{{D}} ={a}^{\mathrm{2}} \left(\mathrm{3}+\mathrm{174tan}^{−\mathrm{1}} \mathrm{2}−\mathrm{17tan}^{−\mathrm{1}} \mathrm{4}\right). \\ $$$$\therefore\:{I}=\left(\frac{−\mathrm{64}}{\mathrm{3}}\right){a}^{\mathrm{2}} +\mathrm{17}{a}^{\mathrm{2}} \mathrm{tan}^{−\mathrm{1}} \mathrm{4} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *