Question-106029

Question Number 106029 by ajfour last updated on 02/Aug/20

Commented by ajfour last updated on 02/Aug/20

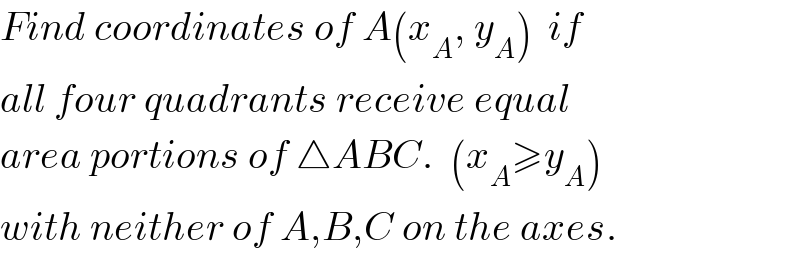
Find coordinates of A(x_A , y_A ) if all four quadrants receive equal area portions of △ABC. (x_A ≥y_A ) with neither of A,B,C on the axes.

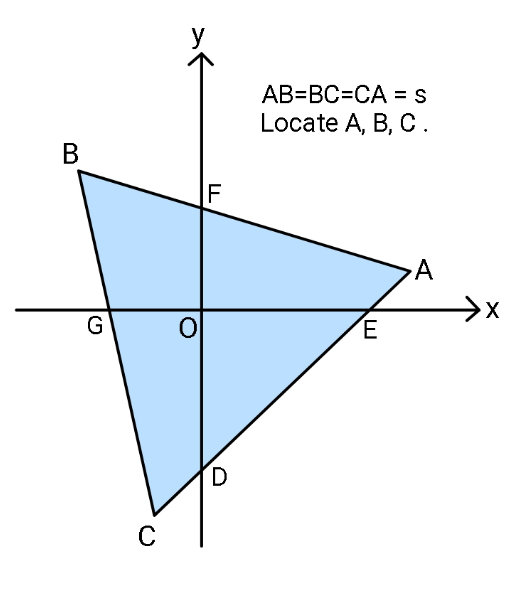
$${Find}\:{coordinates}\:{of}\:{A}\left({x}_{{A}} ,\:{y}_{{A}} \right)\:\:{if} \\ $$$${all}\:{four}\:{quadrants}\:{receive}\:{equal} \\ $$$${area}\:{portions}\:{of}\:\bigtriangleup{ABC}.\:\:\left({x}_{{A}} \geqslant{y}_{{A}} \right) \\ $$$${with}\:{neither}\:{of}\:{A},{B},{C}\:{on}\:{the}\:{axes}. \\ $$

Answered by ajfour last updated on 02/Aug/20

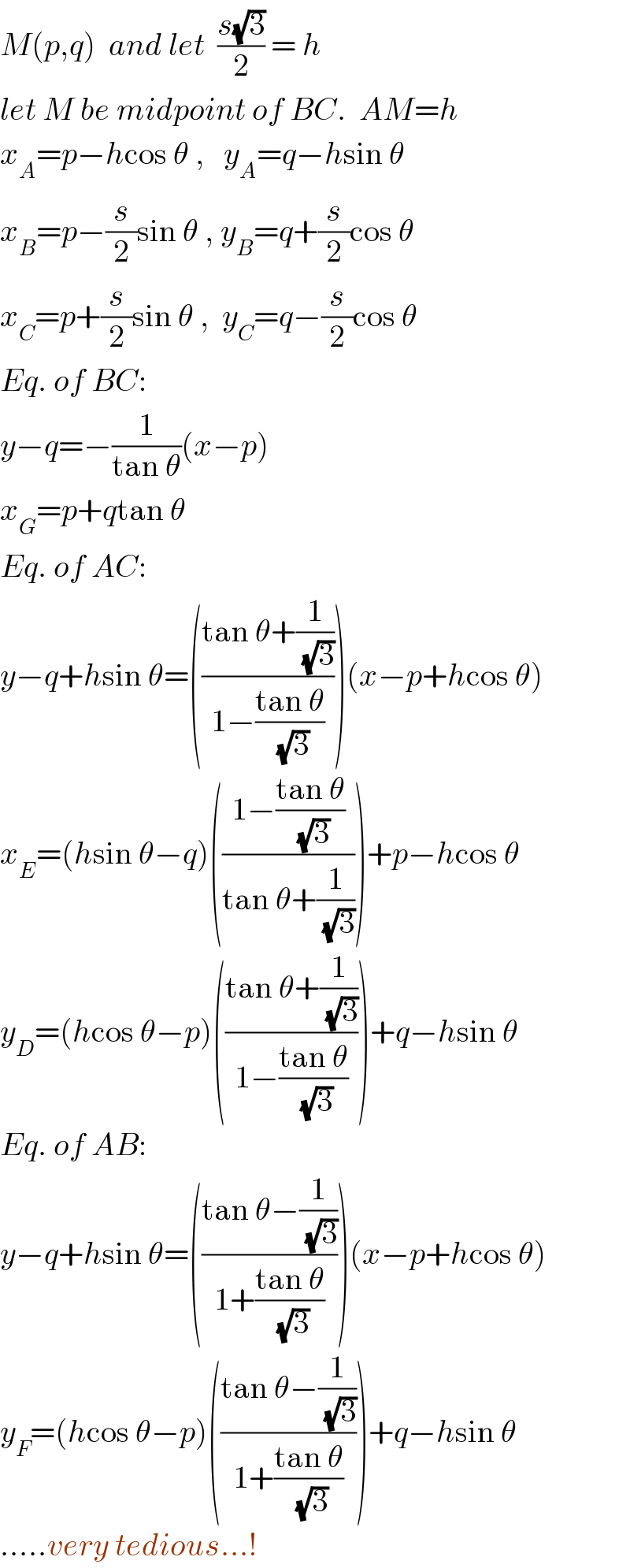
M(p,q) and let ((s(√3))/2) = h let M be midpoint of BC. AM=h x_A =p−hcos θ , y_A =q−hsin θ x_B =p−(s/2)sin θ , y_B =q+(s/2)cos θ x_C =p+(s/2)sin θ , y_C =q−(s/2)cos θ Eq. of BC: y−q=−(1/(tan θ))(x−p) x_G =p+qtan θ Eq. of AC: y−q+hsin θ=(((tan θ+(1/( (√3))))/(1−((tan θ)/( (√3))))))(x−p+hcos θ) x_E =(hsin θ−q)(((1−((tan θ)/( (√3))))/(tan θ+(1/( (√3))))))+p−hcos θ y_D =(hcos θ−p)(((tan θ+(1/( (√3))))/(1−((tan θ)/( (√3))))))+q−hsin θ Eq. of AB: y−q+hsin θ=(((tan θ−(1/( (√3))))/(1+((tan θ)/( (√3))))))(x−p+hcos θ) y_F =(hcos θ−p)(((tan θ−(1/( (√3))))/(1+((tan θ)/( (√3))))))+q−hsin θ .....very tedious...!

$${M}\left({p},{q}\right)\:\:{and}\:{let}\:\:\frac{{s}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\:{h} \\ $$$${let}\:{M}\:{be}\:{midpoint}\:{of}\:{BC}.\:\:{AM}={h} \\ $$$${x}_{{A}} ={p}−{h}\mathrm{cos}\:\theta\:,\:\:\:{y}_{{A}} ={q}−{h}\mathrm{sin}\:\theta \\ $$$${x}_{{B}} ={p}−\frac{{s}}{\mathrm{2}}\mathrm{sin}\:\theta\:,\:{y}_{{B}} ={q}+\frac{{s}}{\mathrm{2}}\mathrm{cos}\:\theta \\ $$$${x}_{{C}} ={p}+\frac{{s}}{\mathrm{2}}\mathrm{sin}\:\theta\:,\:\:{y}_{{C}} ={q}−\frac{{s}}{\mathrm{2}}\mathrm{cos}\:\theta \\ $$$${Eq}.\:{of}\:{BC}: \\ $$$${y}−{q}=−\frac{\mathrm{1}}{\mathrm{tan}\:\theta}\left({x}−{p}\right) \\ $$$${x}_{{G}} ={p}+{q}\mathrm{tan}\:\theta \\ $$$${Eq}.\:{of}\:{AC}: \\ $$$${y}−{q}+{h}\mathrm{sin}\:\theta=\left(\frac{\mathrm{tan}\:\theta+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}−\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{3}}}}\right)\left({x}−{p}+{h}\mathrm{cos}\:\theta\right) \\ $$$${x}_{{E}} =\left({h}\mathrm{sin}\:\theta−{q}\right)\left(\frac{\mathrm{1}−\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{3}}}}{\mathrm{tan}\:\theta+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}\right)+{p}−{h}\mathrm{cos}\:\theta \\ $$$${y}_{{D}} =\left({h}\mathrm{cos}\:\theta−{p}\right)\left(\frac{\mathrm{tan}\:\theta+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}−\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{3}}}}\right)+{q}−{h}\mathrm{sin}\:\theta \\ $$$${Eq}.\:{of}\:{AB}: \\ $$$${y}−{q}+{h}\mathrm{sin}\:\theta=\left(\frac{\mathrm{tan}\:\theta−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{3}}}}\right)\left({x}−{p}+{h}\mathrm{cos}\:\theta\right) \\ $$$${y}_{{F}} =\left({h}\mathrm{cos}\:\theta−{p}\right)\left(\frac{\mathrm{tan}\:\theta−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}+\frac{\mathrm{tan}\:\theta}{\:\sqrt{\mathrm{3}}}}\right)+{q}−{h}\mathrm{sin}\:\theta \\ $$$$…..{very}\:{tedious}…! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply