Menu Close

Show-that-4-3n-2-5-is-divisible-by-9-then-simplify-4-3n-2-5-9-

Tinku Tara 0 Comments
Pin




Question Number 171572 by Raxreedoroid last updated on 18/Jun/22
Show that 4^(3n−2) +5 is divisible by 9 then simplify ((4^(3n−2) +5)/9)
$$\mathrm{Show}\:\mathrm{that} \\ $$$$\mathrm{4}^{\mathrm{3}{n}−\mathrm{2}} +\mathrm{5}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{9} \\ $$$$\mathrm{then}\:\mathrm{simplify}\:\frac{\mathrm{4}^{\mathrm{3}{n}−\mathrm{2}} +\mathrm{5}}{\mathrm{9}} \\ $$
Commented by kaivan.ahmadi last updated on 18/Jun/22
n=1⇒9∣4+5 n=k⇒9∣4^(3k−2) +5 n=k+1⇒4^(3(k+1)−2) +5=4^(3k−2) ×4^3 +5= 4^3 (4^(3k−2) +5)−(4^3 −1)×5= 4^3 (4^(3k−2) +5)−63×5 with hypothesis 9∣4^3 (4^(3k−2) +5) and clearly 9∣63×5 .■
$${n}=\mathrm{1}\Rightarrow\mathrm{9}\mid\mathrm{4}+\mathrm{5} \\ $$$${n}={k}\Rightarrow\mathrm{9}\mid\mathrm{4}^{\mathrm{3}{k}−\mathrm{2}} +\mathrm{5} \\ $$$${n}={k}+\mathrm{1}\Rightarrow\mathrm{4}^{\mathrm{3}\left({k}+\mathrm{1}\right)−\mathrm{2}} +\mathrm{5}=\mathrm{4}^{\mathrm{3}{k}−\mathrm{2}} ×\mathrm{4}^{\mathrm{3}} +\mathrm{5}= \\ $$$$\mathrm{4}^{\mathrm{3}} \left(\mathrm{4}^{\mathrm{3}{k}−\mathrm{2}} +\mathrm{5}\right)−\left(\mathrm{4}^{\mathrm{3}} −\mathrm{1}\right)×\mathrm{5}= \\ $$$$\mathrm{4}^{\mathrm{3}} \left(\mathrm{4}^{\mathrm{3}{k}−\mathrm{2}} +\mathrm{5}\right)−\mathrm{63}×\mathrm{5} \\ $$$${with}\:{hypothesis}\:\mathrm{9}\mid\mathrm{4}^{\mathrm{3}} \left(\mathrm{4}^{\mathrm{3}{k}−\mathrm{2}} +\mathrm{5}\right) \\ $$$${and}\:{clearly}\:\mathrm{9}\mid\mathrm{63}×\mathrm{5}\:\:.\blacksquare \\ $$$$ \\ $$
Answered by floor(10²Eta[1]) last updated on 18/Jun/22
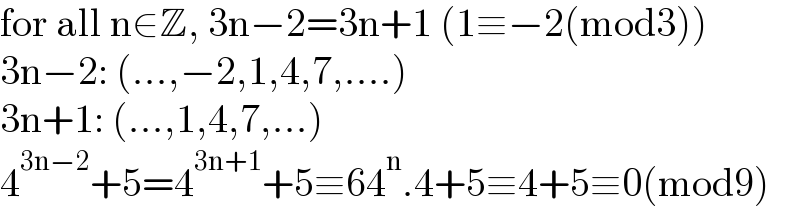
for all n∈Z, 3n−2=3n+1 (1≡−2(mod3)) 3n−2: (...,−2,1,4,7,....) 3n+1: (...,1,4,7,...) 4^(3n−2) +5=4^(3n+1) +5≡64^n .4+5≡4+5≡0(mod9)
$$\mathrm{for}\:\mathrm{all}\:\mathrm{n}\in\mathbb{Z},\:\mathrm{3n}−\mathrm{2}=\mathrm{3n}+\mathrm{1}\:\left(\mathrm{1}\equiv−\mathrm{2}\left(\mathrm{mod3}\right)\right) \\ $$$$\mathrm{3n}−\mathrm{2}:\:\left(…,−\mathrm{2},\mathrm{1},\mathrm{4},\mathrm{7},….\right) \\ $$$$\mathrm{3n}+\mathrm{1}:\:\left(…,\mathrm{1},\mathrm{4},\mathrm{7},…\right) \\ $$$$\mathrm{4}^{\mathrm{3n}−\mathrm{2}} +\mathrm{5}=\mathrm{4}^{\mathrm{3n}+\mathrm{1}} +\mathrm{5}\equiv\mathrm{64}^{\mathrm{n}} .\mathrm{4}+\mathrm{5}\equiv\mathrm{4}+\mathrm{5}\equiv\mathrm{0}\left(\mathrm{mod9}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *