Question Number 106044 by ZiYangLee last updated on 02/Aug/20
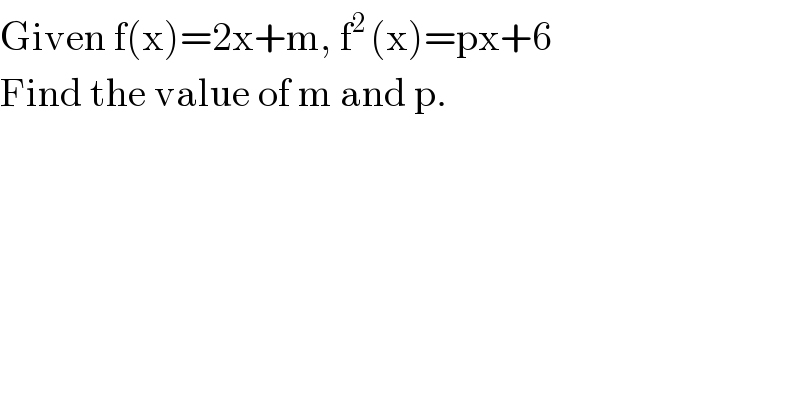
$$\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2x}+\mathrm{m},\:\mathrm{f}^{\mathrm{2}\:} \left(\mathrm{x}\right)=\mathrm{px}+\mathrm{6} \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{m}\:\mathrm{and}\:\mathrm{p}. \\ $$
Answered by 1549442205PVT last updated on 02/Aug/20
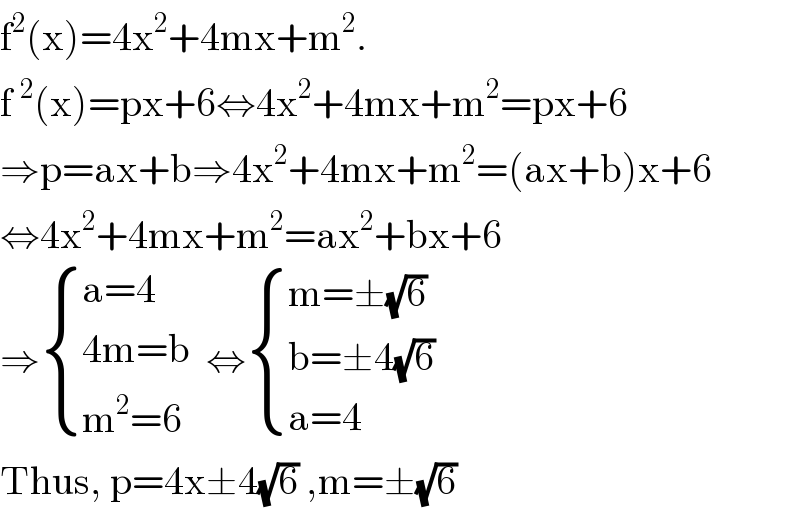
$$\mathrm{f}^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{4x}^{\mathrm{2}} +\mathrm{4mx}+\mathrm{m}^{\mathrm{2}} . \\ $$$$\mathrm{f}\:^{\mathrm{2}} \left(\mathrm{x}\right)=\mathrm{px}+\mathrm{6}\Leftrightarrow\mathrm{4x}^{\mathrm{2}} +\mathrm{4mx}+\mathrm{m}^{\mathrm{2}} =\mathrm{px}+\mathrm{6} \\ $$$$\Rightarrow\mathrm{p}=\mathrm{ax}+\mathrm{b}\Rightarrow\mathrm{4x}^{\mathrm{2}} +\mathrm{4mx}+\mathrm{m}^{\mathrm{2}} =\left(\mathrm{ax}+\mathrm{b}\right)\mathrm{x}+\mathrm{6} \\ $$$$\Leftrightarrow\mathrm{4x}^{\mathrm{2}} +\mathrm{4mx}+\mathrm{m}^{\mathrm{2}} =\mathrm{ax}^{\mathrm{2}} +\mathrm{bx}+\mathrm{6} \\ $$$$\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{4}}\\{\mathrm{4m}=\mathrm{b}}\\{\mathrm{m}^{\mathrm{2}} =\mathrm{6}}\end{cases}\:\:\Leftrightarrow\begin{cases}{\mathrm{m}=\pm\sqrt{\mathrm{6}}}\\{\mathrm{b}=\pm\mathrm{4}\sqrt{\mathrm{6}}}\\{\mathrm{a}=\mathrm{4}}\end{cases} \\ $$$$\mathrm{Thus},\:\mathrm{p}=\mathrm{4x}\pm\mathrm{4}\sqrt{\mathrm{6}}\:,\mathrm{m}=\pm\sqrt{\mathrm{6}} \\ $$
Commented by ZiYangLee last updated on 03/Aug/20

$$\mathrm{thanks}\:<\mathrm{3} \\ $$
