Menu Close

Determine-x-amp-y-such-that-lcm-x-y-gcd-x-y-x-y-

Tinku Tara 0 Comments
Pin




Question Number 106222 by Rasheed.Sindhi last updated on 03/Aug/20
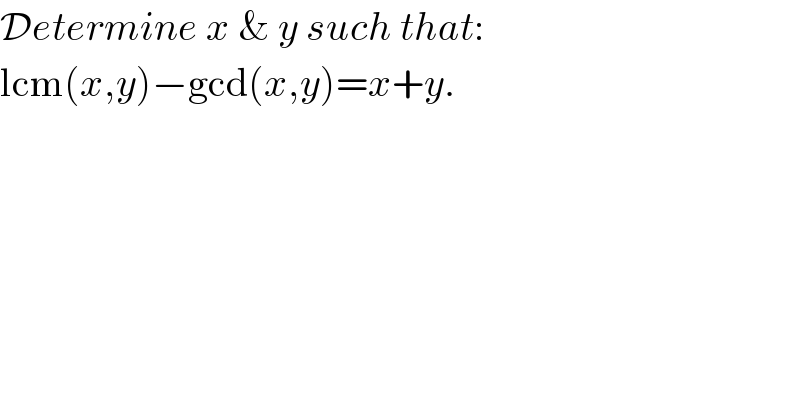
Determine x & y such that: lcm(x,y)−gcd(x,y)=x+y.
$$\mathcal{D}{etermine}\:{x}\:\&\:{y}\:{such}\:{that}: \\ $$$$\mathrm{lcm}\left({x},{y}\right)−\mathrm{gcd}\left({x},{y}\right)={x}+{y}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Aug/20
Thanks sir 〽️�� ��
Commented by Rasheed.Sindhi last updated on 03/Aug/20
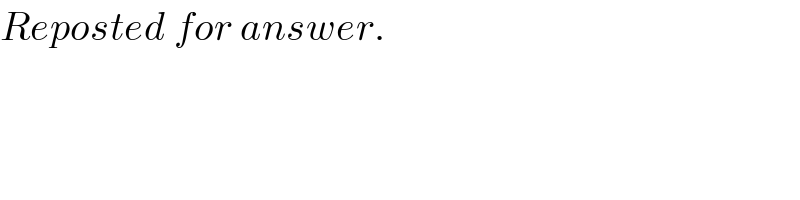
Reposted for answer.
$${Reposted}\:{for}\:{answer}. \\ $$
Commented by mr W last updated on 03/Aug/20
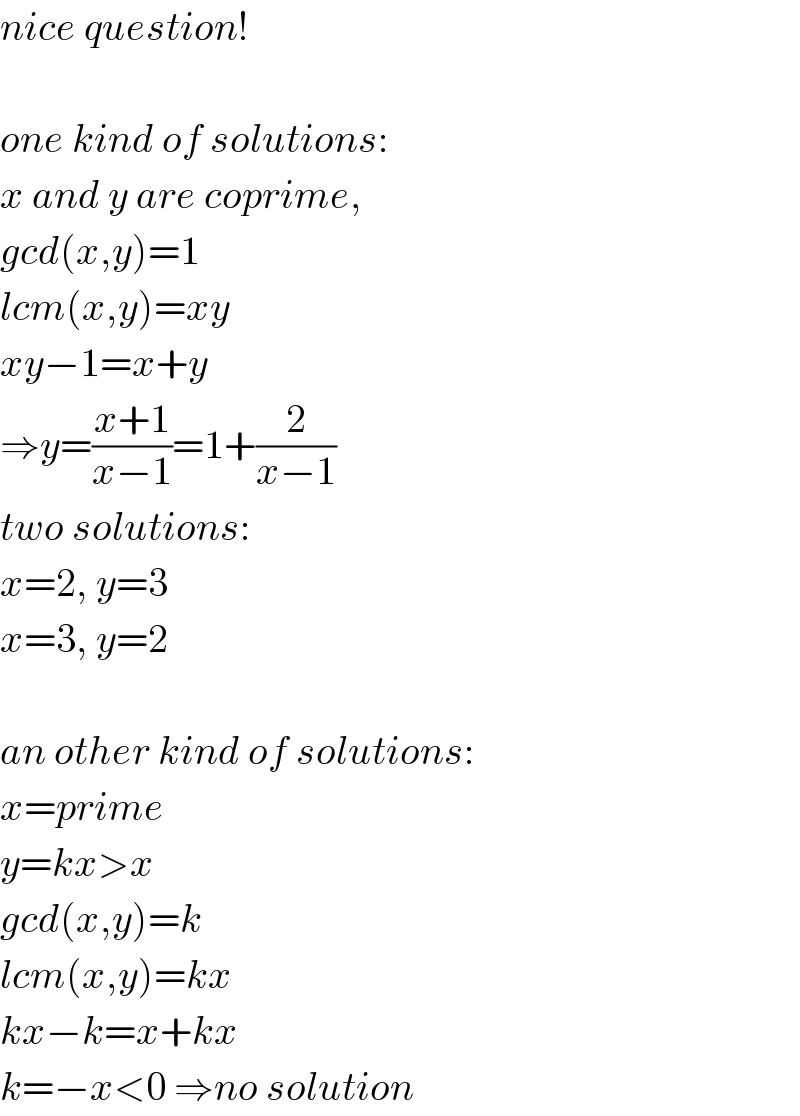
nice question! one kind of solutions: x and y are coprime, gcd(x,y)=1 lcm(x,y)=xy xy−1=x+y ⇒y=((x+1)/(x−1))=1+(2/(x−1)) two solutions: x=2, y=3 x=3, y=2 an other kind of solutions: x=prime y=kx>x gcd(x,y)=k lcm(x,y)=kx kx−k=x+kx k=−x<0 ⇒no solution
$${nice}\:{question}! \\ $$$$ \\ $$$${one}\:{kind}\:{of}\:{solutions}: \\ $$$${x}\:{and}\:{y}\:{are}\:{coprime},\: \\ $$$${gcd}\left({x},{y}\right)=\mathrm{1} \\ $$$${lcm}\left({x},{y}\right)={xy} \\ $$$${xy}−\mathrm{1}={x}+{y} \\ $$$$\Rightarrow{y}=\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}=\mathrm{1}+\frac{\mathrm{2}}{{x}−\mathrm{1}} \\ $$$${two}\:{solutions}: \\ $$$${x}=\mathrm{2},\:{y}=\mathrm{3} \\ $$$${x}=\mathrm{3},\:{y}=\mathrm{2} \\ $$$$ \\ $$$${an}\:{other}\:{kind}\:{of}\:{solutions}: \\ $$$${x}={prime} \\ $$$${y}={kx}>{x} \\ $$$${gcd}\left({x},{y}\right)={k} \\ $$$${lcm}\left({x},{y}\right)={kx} \\ $$$${kx}−{k}={x}+{kx} \\ $$$${k}=−{x}<\mathrm{0}\:\Rightarrow{no}\:{solution} \\ $$
Commented by Rasheed.Sindhi last updated on 03/Aug/20
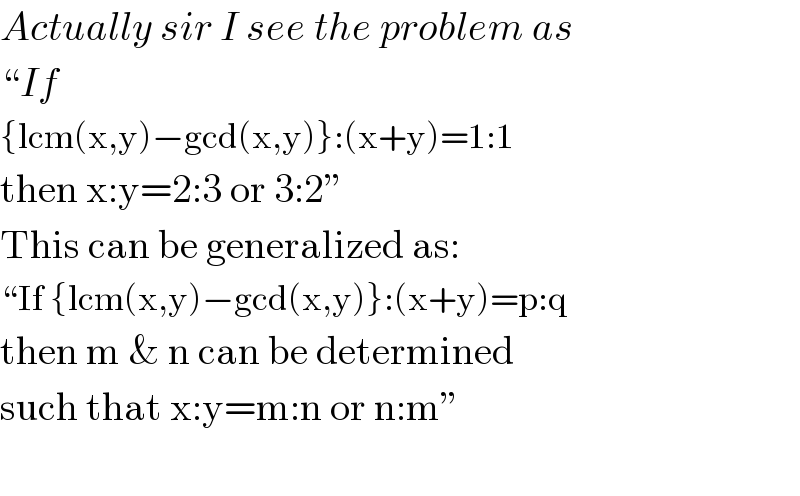
Actually sir I see the problem as “If {lcm(x,y)−gcd(x,y)}:(x+y)=1:1 then x:y=2:3 or 3:2” This can be generalized as: “If {lcm(x,y)−gcd(x,y)}:(x+y)=p:q then m & n can be determined such that x:y=m:n or n:m”
$${Actually}\:{sir}\:{I}\:{see}\:{the}\:{problem}\:{as} \\ $$$$“{If} \\ $$$$\left\{\mathrm{lcm}\left(\mathrm{x},\mathrm{y}\right)−\mathrm{gcd}\left(\mathrm{x},\mathrm{y}\right)\right\}:\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{1}:\mathrm{1} \\ $$$$\mathrm{then}\:\mathrm{x}:\mathrm{y}=\mathrm{2}:\mathrm{3}\:\mathrm{or}\:\mathrm{3}:\mathrm{2}'' \\ $$$$\mathrm{This}\:\mathrm{can}\:\mathrm{be}\:\mathrm{generalized}\:\mathrm{as}: \\ $$$$“\mathrm{If}\:\left\{\mathrm{lcm}\left(\mathrm{x},\mathrm{y}\right)−\mathrm{gcd}\left(\mathrm{x},\mathrm{y}\right)\right\}:\left(\mathrm{x}+\mathrm{y}\right)=\mathrm{p}:\mathrm{q} \\ $$$$\mathrm{then}\:\mathrm{m}\:\&\:\mathrm{n}\:\mathrm{can}\:\mathrm{be}\:\mathrm{determined} \\ $$$$\mathrm{such}\:\mathrm{that}\:\mathrm{x}:\mathrm{y}=\mathrm{m}:\mathrm{n}\:\mathrm{or}\:\mathrm{n}:\mathrm{m}'' \\ $$$$ \\ $$
Commented by mr W last updated on 03/Aug/20
yes sir, great solution!
$${yes}\:{sir},\:{great}\:{solution}! \\ $$
Answered by Rasheed.Sindhi last updated on 03/Aug/20
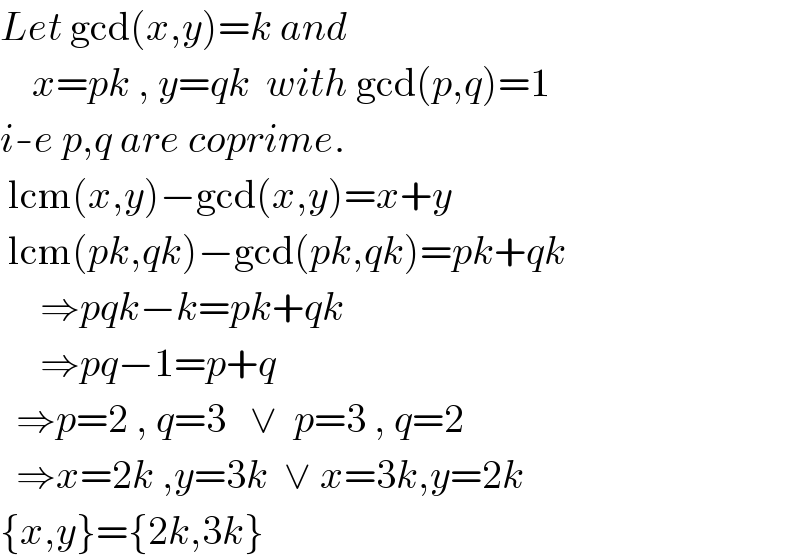
Let gcd(x,y)=k and x=pk , y=qk with gcd(p,q)=1 i-e p,q are coprime. lcm(x,y)−gcd(x,y)=x+y lcm(pk,qk)−gcd(pk,qk)=pk+qk ⇒pqk−k=pk+qk ⇒pq−1=p+q ⇒p=2 , q=3 ∨ p=3 , q=2 ⇒x=2k ,y=3k ∨ x=3k,y=2k {x,y}={2k,3k}
$${Let}\:\mathrm{gcd}\left({x},{y}\right)={k}\:{and} \\ $$$$\:\:\:\:{x}={pk}\:,\:{y}={qk}\:\:{with}\:\mathrm{gcd}\left({p},{q}\right)=\mathrm{1} \\ $$$${i}-{e}\:{p},{q}\:{are}\:{coprime}. \\ $$$$\:\mathrm{lcm}\left({x},{y}\right)−\mathrm{gcd}\left({x},{y}\right)={x}+{y} \\ $$$$\:\mathrm{lcm}\left({pk},{qk}\right)−\mathrm{gcd}\left({pk},{qk}\right)={pk}+{qk} \\ $$$$\:\:\:\:\:\Rightarrow{pqk}−{k}={pk}+{qk} \\ $$$$\:\:\:\:\:\Rightarrow{pq}−\mathrm{1}={p}+{q} \\ $$$$\:\:\Rightarrow{p}=\mathrm{2}\:,\:{q}=\mathrm{3}\:\:\:\vee\:\:{p}=\mathrm{3}\:,\:{q}=\mathrm{2} \\ $$$$\:\:\Rightarrow{x}=\mathrm{2}{k}\:,{y}=\mathrm{3}{k}\:\:\vee\:{x}=\mathrm{3}{k},{y}=\mathrm{2}{k} \\ $$$$\left\{{x},{y}\right\}=\left\{\mathrm{2}{k},\mathrm{3}{k}\right\} \\ $$
Commented by Rasheed.Sindhi last updated on 03/Aug/20
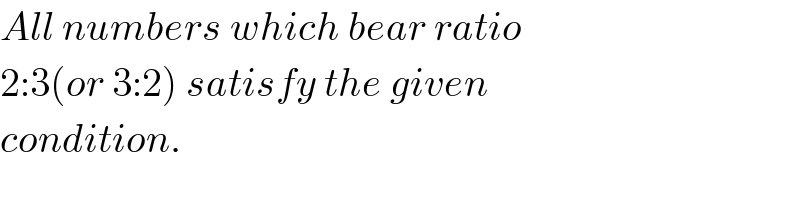
All numbers which bear ratio 2:3(or 3:2) satisfy the given condition.
$${All}\:{numbers}\:{which}\:{bear}\:{ratio} \\ $$$$\mathrm{2}:\mathrm{3}\left({or}\:\mathrm{3}:\mathrm{2}\right)\:{satisfy}\:{the}\:{given} \\ $$$${condition}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Aug/20
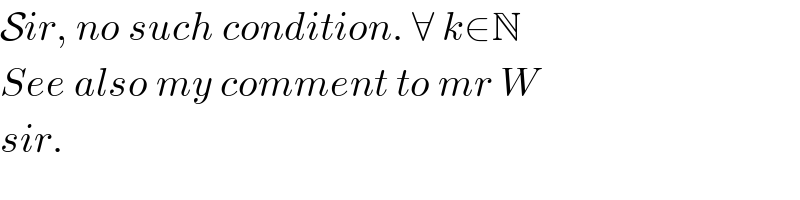
Sir, no such condition. ∀ k∈N See also my comment to mr W sir.
$$\mathcal{S}{ir},\:{no}\:{such}\:{condition}.\:\forall\:{k}\in\mathbb{N} \\ $$$${See}\:{also}\:{my}\:{comment}\:{to}\:{mr}\:{W} \\ $$$${sir}. \\ $$
Commented by Rasheed.Sindhi last updated on 03/Aug/20
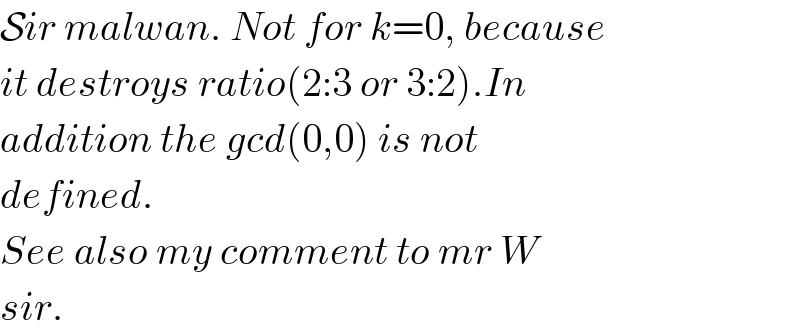
Sir malwan. Not for k=0, because it destroys ratio(2:3 or 3:2).In addition the gcd(0,0) is not defined. See also my comment to mr W sir.
$$\mathcal{S}{ir}\:{malwan}.\:{Not}\:{for}\:{k}=\mathrm{0},\:{because} \\ $$$${it}\:{destroys}\:{ratio}\left(\mathrm{2}:\mathrm{3}\:{or}\:\mathrm{3}:\mathrm{2}\right).{In} \\ $$$${addition}\:{the}\:{gcd}\left(\mathrm{0},\mathrm{0}\right)\:{is}\:{not} \\ $$$${defined}. \\ $$$${See}\:{also}\:{my}\:{comment}\:{to}\:{mr}\:{W} \\ $$$${sir}. \\ $$
Commented by PRITHWISH SEN 2 last updated on 03/Aug/20
Nice sir
$$\mathrm{Nice}\:\mathrm{sir} \\ $$
Commented by malwaan last updated on 03/Aug/20
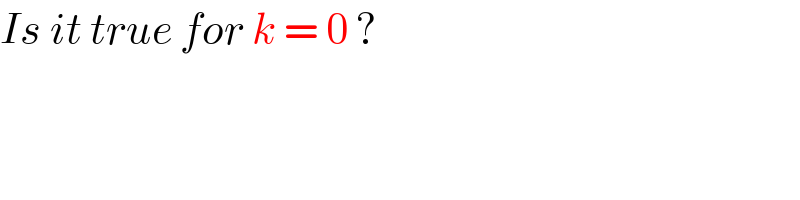
Is it true for k = 0 ?
$${Is}\:{it}\:{true}\:{for}\:{k}\:=\:\mathrm{0}\:? \\ $$
Commented by PRITHWISH SEN 2 last updated on 03/Aug/20
Is there any certain condition that k should be prime or it is true for all natural numbers ?
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{certain}\:\mathrm{condition}\:\mathrm{that}\:\mathrm{k}\:\mathrm{should}\:\mathrm{be} \\ $$$$\mathrm{prime}\:\mathrm{or}\:\mathrm{it}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:\mathrm{natural}\:\mathrm{numbers}\:? \\ $$
Commented by malwaan last updated on 04/Aug/20
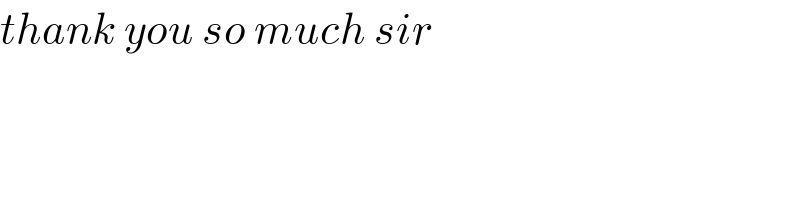
thank you so much sir
$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *