Menu Close

calculate-lim-x-0-cos-x-sinx-1-x-2-

Tinku Tara 0 Comments
Pin




Question Number 40709 by math khazana by abdo last updated on 26/Jul/18
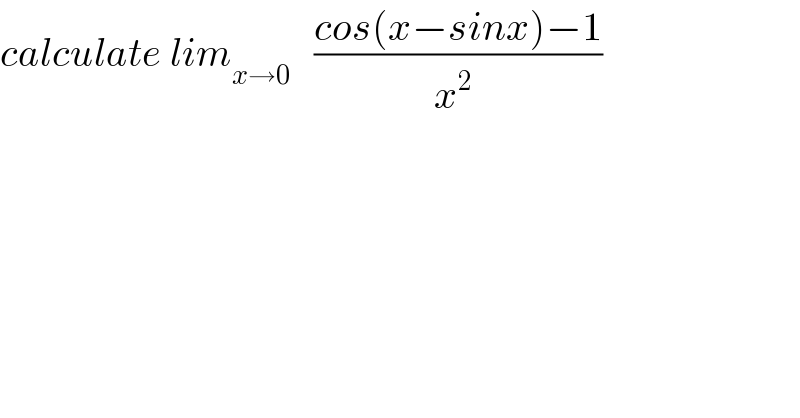
calculate lim_(x→0) ((cos(x−sinx)−1)/(x^2 ))
$${calculate}\:{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{cos}\left({x}−{sinx}\right)−\mathrm{1}}{{x}^{\mathrm{2}} \:} \\ $$
Commented by maxmathsup by imad last updated on 26/Jul/18
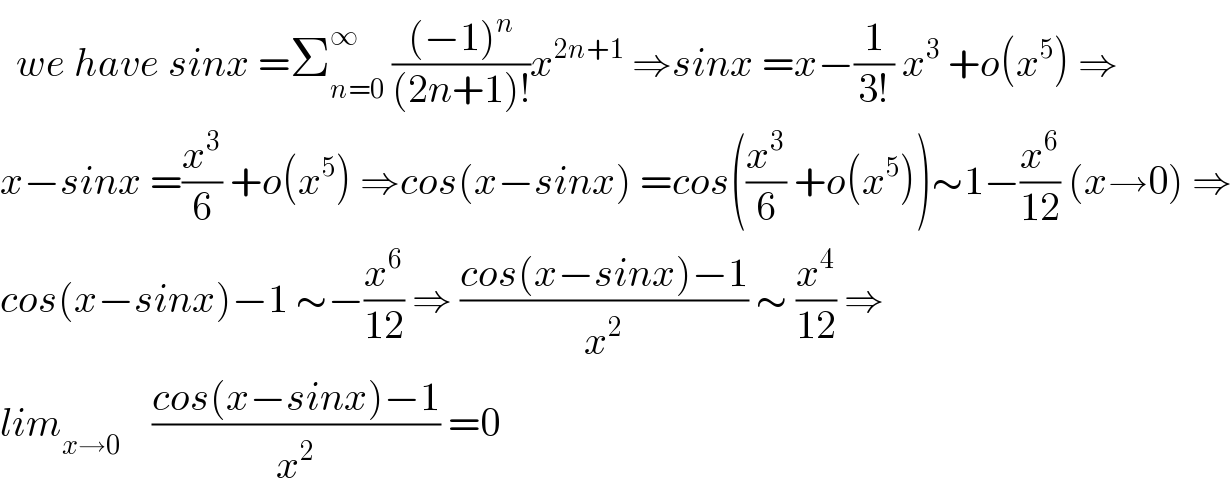
we have sinx =Σ_(n=0) ^∞ (((−1)^n )/((2n+1)!))x^(2n+1) ⇒sinx =x−(1/(3!)) x^3 +o(x^5 ) ⇒ x−sinx =(x^3 /6) +o(x^5 ) ⇒cos(x−sinx) =cos((x^3 /6) +o(x^5 ))∼1−(x^6 /(12)) (x→0) ⇒ cos(x−sinx)−1 ∼−(x^6 /(12)) ⇒ ((cos(x−sinx)−1)/x^2 ) ∼ (x^4 /(12)) ⇒ lim_(x→0) ((cos(x−sinx)−1)/x^2 ) =0
$$\:\:{we}\:{have}\:{sinx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}{x}^{\mathrm{2}{n}+\mathrm{1}} \:\Rightarrow{sinx}\:={x}−\frac{\mathrm{1}}{\mathrm{3}!}\:{x}^{\mathrm{3}} \:+{o}\left({x}^{\mathrm{5}} \right)\:\Rightarrow \\ $$$${x}−{sinx}\:=\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{5}} \right)\:\Rightarrow{cos}\left({x}−{sinx}\right)\:={cos}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{6}}\:+{o}\left({x}^{\mathrm{5}} \right)\right)\sim\mathrm{1}−\frac{{x}^{\mathrm{6}} }{\mathrm{12}}\:\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$${cos}\left({x}−{sinx}\right)−\mathrm{1}\:\sim−\frac{{x}^{\mathrm{6}} }{\mathrm{12}}\:\Rightarrow\:\frac{{cos}\left({x}−{sinx}\right)−\mathrm{1}}{{x}^{\mathrm{2}} }\:\sim\:\frac{{x}^{\mathrm{4}} }{\mathrm{12}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{{cos}\left({x}−{sinx}\right)−\mathrm{1}}{{x}^{\mathrm{2}} }\:=\mathrm{0} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Jul/18
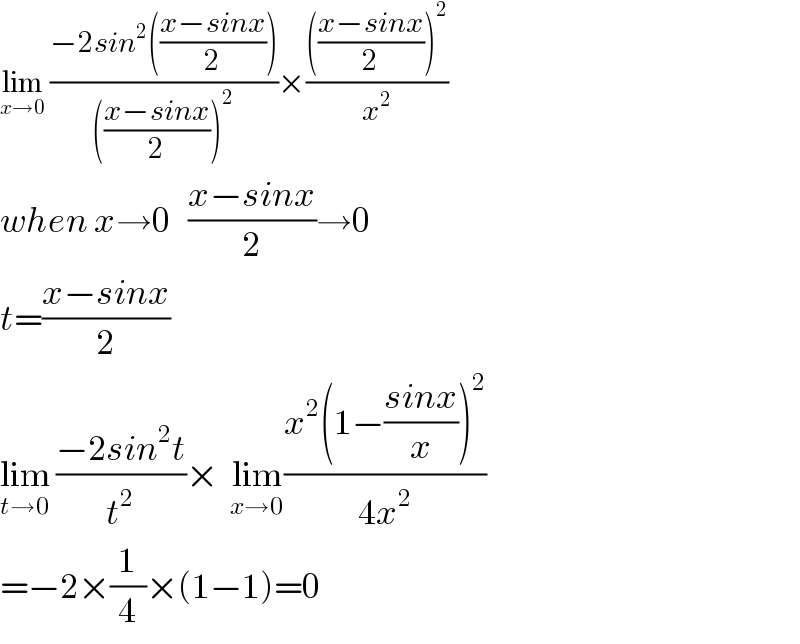
lim_(x→0) ((−2sin^2 (((x−sinx)/2)))/((((x−sinx)/2))^2 ))×(((((x−sinx)/2))^2 )/x^2 ) when x→0 ((x−sinx)/2)→0 t=((x−sinx)/2) lim_(t→0) ((−2sin^2 t)/t^2 )× lim_(x→0) ((x^2 (1−((sinx)/x))^2 )/(4x^2 )) =−2×(1/4)×(1−1)=0
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{x}−{sinx}}{\mathrm{2}}\right)}{\left(\frac{{x}−{sinx}}{\mathrm{2}}\right)^{\mathrm{2}} }×\frac{\left(\frac{{x}−{sinx}}{\mathrm{2}}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$${when}\:{x}\rightarrow\mathrm{0}\:\:\:\frac{{x}−{sinx}}{\mathrm{2}}\rightarrow\mathrm{0} \\ $$$${t}=\frac{{x}−{sinx}}{\mathrm{2}} \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2}{sin}^{\mathrm{2}} {t}}{{t}^{\mathrm{2}} }×\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}^{\mathrm{2}} \left(\mathrm{1}−\frac{{sinx}}{{x}}\right)^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} } \\ $$$$=−\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}×\left(\mathrm{1}−\mathrm{1}\right)=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *