Question Number 106315 by pticantor last updated on 04/Aug/20
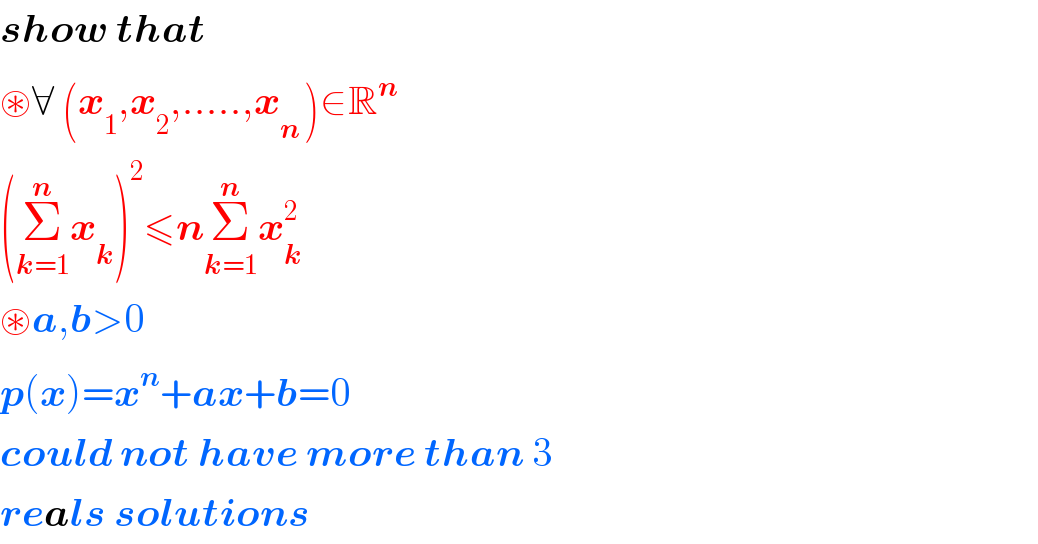
$$\boldsymbol{{show}}\:\boldsymbol{{that}} \\ $$$$\circledast\forall\:\left(\boldsymbol{{x}}_{\mathrm{1}} ,\boldsymbol{{x}}_{\mathrm{2}} ,…..,\boldsymbol{{x}}_{\boldsymbol{{n}}\:} \right)\in\mathbb{R}^{\boldsymbol{{n}}} \\ $$$$\left(\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\boldsymbol{{x}}_{\boldsymbol{{k}}} \right)^{\mathrm{2}} \leqslant\boldsymbol{{n}}\underset{\boldsymbol{{k}}=\mathrm{1}} {\overset{\boldsymbol{{n}}} {\sum}}\boldsymbol{{x}}_{\boldsymbol{{k}}} ^{\mathrm{2}} \\ $$$$\circledast\boldsymbol{{a}},\boldsymbol{{b}}>\mathrm{0} \\ $$$$\boldsymbol{{p}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{x}}^{\boldsymbol{{n}}} +\boldsymbol{{ax}}+\boldsymbol{{b}}=\mathrm{0} \\ $$$$\boldsymbol{{could}}\:\boldsymbol{{not}}\:\boldsymbol{{have}}\:\boldsymbol{{more}}\:\boldsymbol{{than}}\:\mathrm{3} \\ $$$$\boldsymbol{{reals}}\:\boldsymbol{{solutions}} \\ $$
Answered by Dwaipayan Shikari last updated on 04/Aug/20
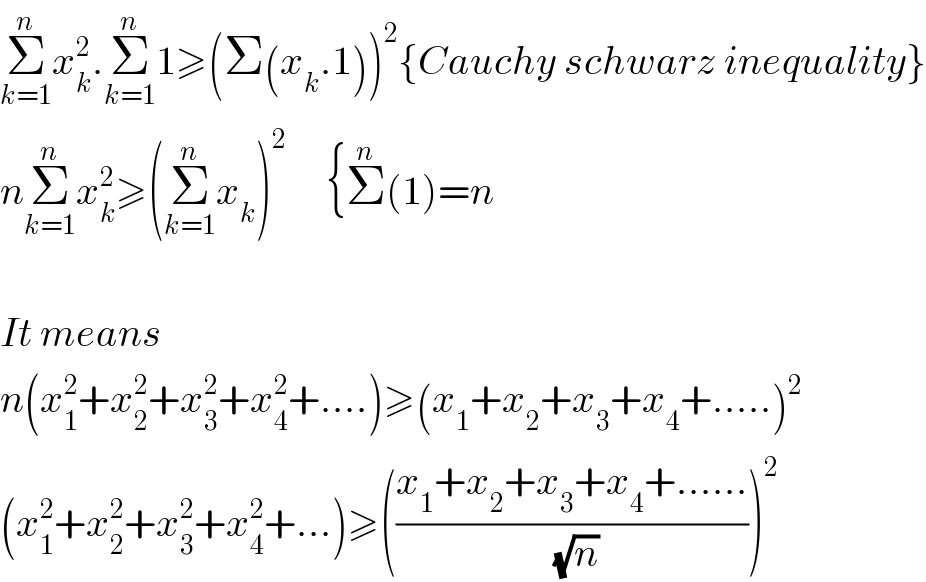
$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} ^{\mathrm{2}} .\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1}\geqslant\left(\Sigma\left({x}_{{k}} .\mathrm{1}\right)\right)^{\mathrm{2}} \left\{{Cauchy}\:{schwarz}\:{inequality}\right\} \\ $$$${n}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} ^{\mathrm{2}} \geqslant\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{k}} \right)^{\mathrm{2}} \:\:\:\:\:\left\{\overset{{n}} {\sum}\left(\mathrm{1}\right)={n}\right. \\ $$$$ \\ $$$${It}\:{means} \\ $$$${n}\left({x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} +{x}_{\mathrm{4}} ^{\mathrm{2}} +….\right)\geqslant\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} +…..\right)^{\mathrm{2}} \\ $$$$\left({x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} +{x}_{\mathrm{4}} ^{\mathrm{2}} +…\right)\geqslant\left(\frac{{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} +……}{\:\sqrt{{n}}}\right)^{\mathrm{2}} \\ $$
