Question Number 69593 by ahmadshahhimat775@gmail.com last updated on 25/Sep/19

Commented by mathmax by abdo last updated on 25/Sep/19
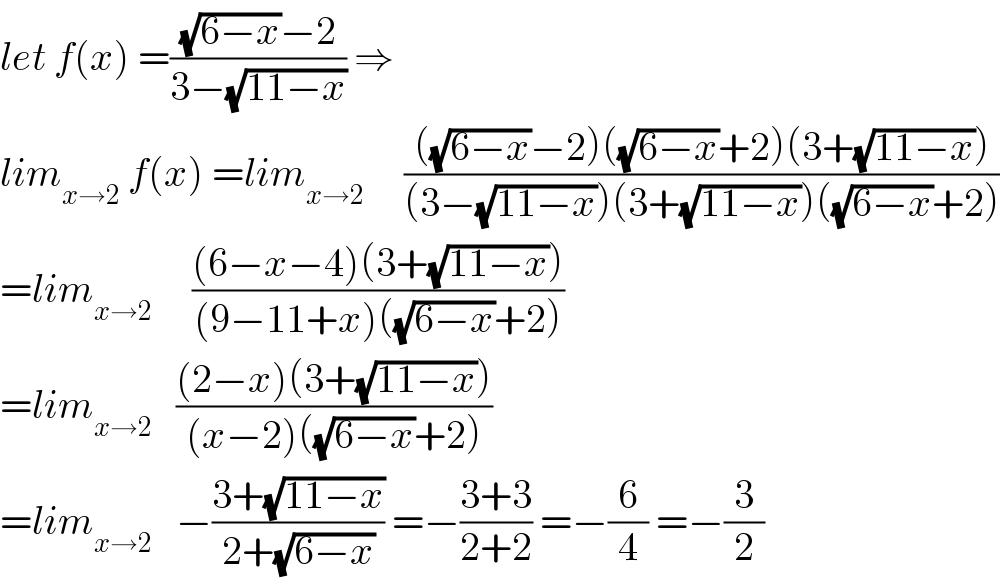
$${let}\:{f}\left({x}\right)\:=\frac{\sqrt{\mathrm{6}−{x}}−\mathrm{2}}{\mathrm{3}−\sqrt{\mathrm{11}−{x}}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{2}} \:{f}\left({x}\right)\:={lim}_{{x}\rightarrow\mathrm{2}} \:\:\:\:\:\frac{\left(\sqrt{\mathrm{6}−{x}}−\mathrm{2}\right)\left(\sqrt{\mathrm{6}−{x}}+\mathrm{2}\right)\left(\mathrm{3}+\sqrt{\mathrm{11}−{x}}\right)}{\left(\mathrm{3}−\sqrt{\mathrm{11}−{x}}\right)\left(\mathrm{3}+\sqrt{\mathrm{11}−{x}}\right)\left(\sqrt{\mathrm{6}−{x}}+\mathrm{2}\right)} \\ $$$$={lim}_{{x}\rightarrow\mathrm{2}} \:\:\:\:\:\frac{\left(\mathrm{6}−{x}−\mathrm{4}\right)\left(\mathrm{3}+\sqrt{\mathrm{11}−{x}}\right)}{\left(\mathrm{9}−\mathrm{11}+{x}\right)\left(\sqrt{\mathrm{6}−{x}}+\mathrm{2}\right)} \\ $$$$={lim}_{{x}\rightarrow\mathrm{2}} \:\:\:\frac{\left(\mathrm{2}−{x}\right)\left(\mathrm{3}+\sqrt{\mathrm{11}−{x}}\right)}{\left({x}−\mathrm{2}\right)\left(\sqrt{\mathrm{6}−{x}}+\mathrm{2}\right)}\: \\ $$$$={lim}_{{x}\rightarrow\mathrm{2}} \:\:\:−\frac{\mathrm{3}+\sqrt{\mathrm{11}−{x}}}{\mathrm{2}+\sqrt{\mathrm{6}−{x}}}\:=−\frac{\mathrm{3}+\mathrm{3}}{\mathrm{2}+\mathrm{2}}\:=−\frac{\mathrm{6}}{\mathrm{4}}\:=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 26/Sep/19

$${V}\:{nice}! \\ $$
Answered by MJS last updated on 25/Sep/19
![lim_(x→2) (((√(6−x))−2)/(3−(√(11−x))))=lim_(x→2) (((d/dx)[(√(6−x))−2])/((d/dx)[3−(√(11−x))]))= =−lim_(x→2) ((√(11−x))/( (√(6−x))))=−(3/2)](https://www.tinkutara.com/question/Q69596.png)
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\sqrt{\mathrm{6}−{x}}−\mathrm{2}}{\mathrm{3}−\sqrt{\mathrm{11}−{x}}}=\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\frac{{d}}{{dx}}\left[\sqrt{\mathrm{6}−{x}}−\mathrm{2}\right]}{\frac{{d}}{{dx}}\left[\mathrm{3}−\sqrt{\mathrm{11}−{x}}\right]}= \\ $$$$=−\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\frac{\sqrt{\mathrm{11}−{x}}}{\:\sqrt{\mathrm{6}−{x}}}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$
