Question Number 40895 by abdo.msup.com last updated on 28/Jul/18
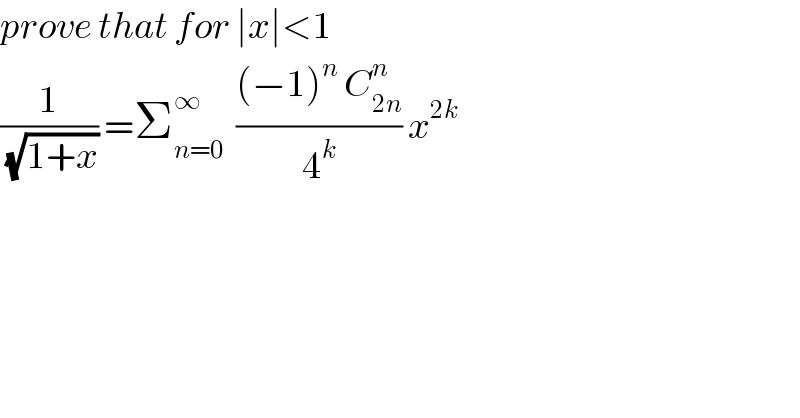
$${prove}\:{that}\:{for}\:\mid{x}\mid<\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+{x}}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} \:{C}_{\mathrm{2}{n}} ^{{n}} }{\mathrm{4}^{{k}} }\:{x}^{\mathrm{2}{k}} \\ $$
