Question Number 171993 by Tawa11 last updated on 23/Jun/22

Commented by Tawa11 last updated on 23/Jun/22

$$\mathrm{A}\:\mathrm{soldier}\:\mathrm{fires}\:\mathrm{shots}\:\mathrm{from}\:\mathrm{his}\:\mathrm{rifle}\:\mathrm{and}\:\mathrm{he}\:\mathrm{is}\:\mathrm{expected}\:\mathrm{to}\:\mathrm{hit}\:\mathrm{a}\:\mathrm{target}\:\:\mathrm{5}\:\:\mathrm{out}\:\mathrm{of}\:\:\mathrm{6} \\ $$$$\mathrm{shots}.\:\mathrm{If}\:\mathrm{the}\:\mathrm{soldier}\:\mathrm{fires}\:\mathrm{five}\:\mathrm{shots},\:\mathrm{find}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{he}\:\mathrm{will} \\ $$$$\left(\mathrm{a}\right)\:\:\mathrm{miss}\:\mathrm{each}\:\mathrm{time} \\ $$$$\left(\mathrm{b}\right)\:\:\mathrm{hit}\:\mathrm{the}\:\mathrm{target}\:\mathrm{thrice} \\ $$$$\left(\mathrm{c}\right)\:\:\mathrm{hit}\:\mathrm{the}\:\mathrm{target}\:\mathrm{at}\:\mathrm{most}\:\mathrm{twice} \\ $$
Commented by mr W last updated on 25/Jun/22
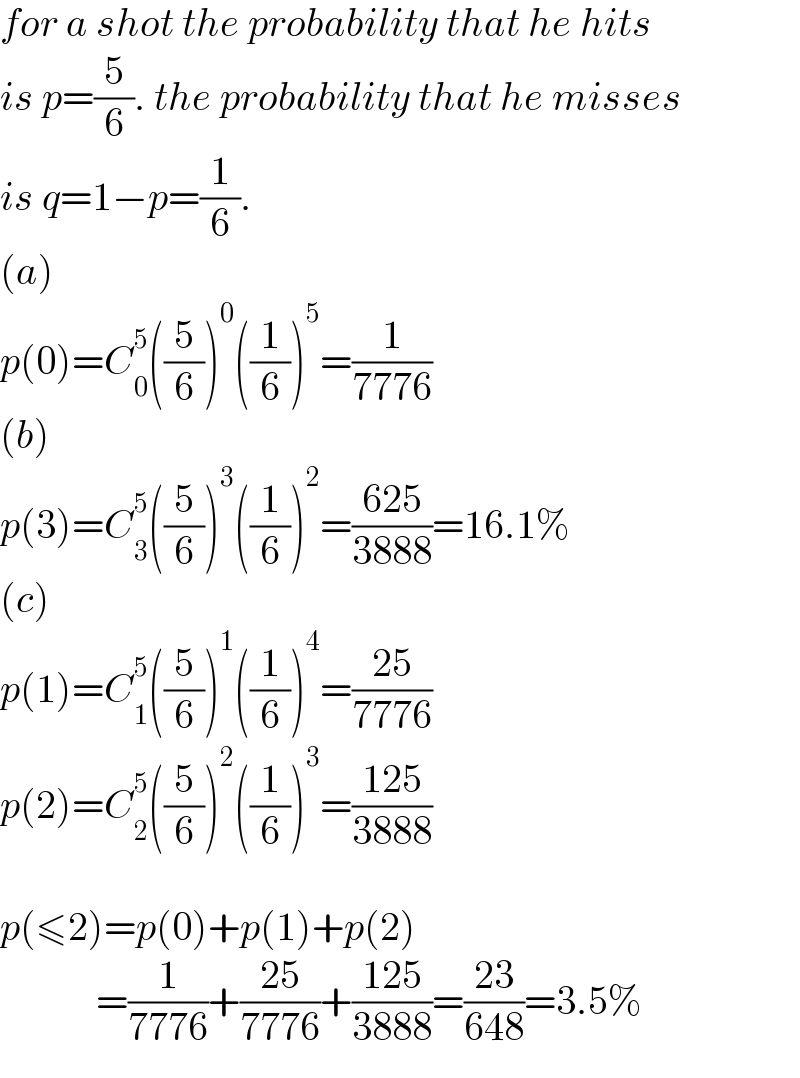
$${for}\:{a}\:{shot}\:{the}\:{probability}\:{that}\:{he}\:{hits} \\ $$$${is}\:{p}=\frac{\mathrm{5}}{\mathrm{6}}.\:{the}\:{probability}\:{that}\:{he}\:{misses} \\ $$$${is}\:{q}=\mathrm{1}−{p}=\frac{\mathrm{1}}{\mathrm{6}}. \\ $$$$\left({a}\right) \\ $$$${p}\left(\mathrm{0}\right)={C}_{\mathrm{0}} ^{\mathrm{5}} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{7776}} \\ $$$$\left({b}\right) \\ $$$${p}\left(\mathrm{3}\right)={C}_{\mathrm{3}} ^{\mathrm{5}} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{2}} =\frac{\mathrm{625}}{\mathrm{3888}}=\mathrm{16}.\mathrm{1\%} \\ $$$$\left({c}\right) \\ $$$${p}\left(\mathrm{1}\right)={C}_{\mathrm{1}} ^{\mathrm{5}} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{4}} =\frac{\mathrm{25}}{\mathrm{7776}} \\ $$$${p}\left(\mathrm{2}\right)={C}_{\mathrm{2}} ^{\mathrm{5}} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)^{\mathrm{3}} =\frac{\mathrm{125}}{\mathrm{3888}} \\ $$$$ \\ $$$${p}\left(\leqslant\mathrm{2}\right)={p}\left(\mathrm{0}\right)+{p}\left(\mathrm{1}\right)+{p}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{7776}}+\frac{\mathrm{25}}{\mathrm{7776}}+\frac{\mathrm{125}}{\mathrm{3888}}=\frac{\mathrm{23}}{\mathrm{648}}=\mathrm{3}.\mathrm{5\%} \\ $$
Commented by Tawa11 last updated on 25/Jun/22
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}. \\ $$
