Question Number 106614 by bemath last updated on 06/Aug/20
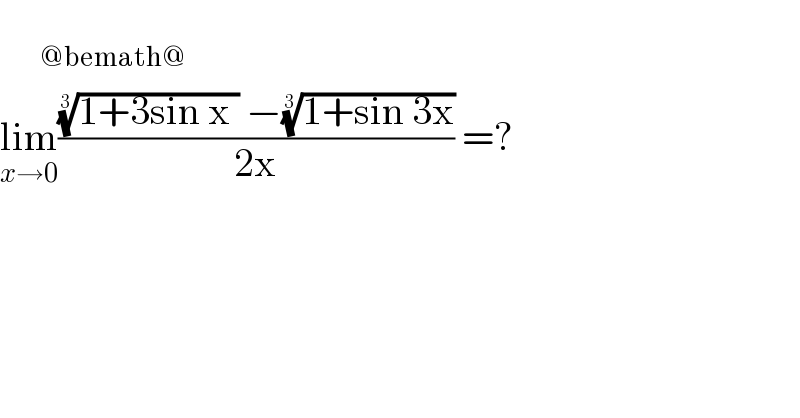
$$\:\:\:\:\:\underset{@\mathrm{bemath}@} {\:} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3sin}\:\mathrm{x}\:}\:−\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{3x}}}{\mathrm{2x}}\:=?\: \\ $$
Answered by Dwaipayan Shikari last updated on 06/Aug/20
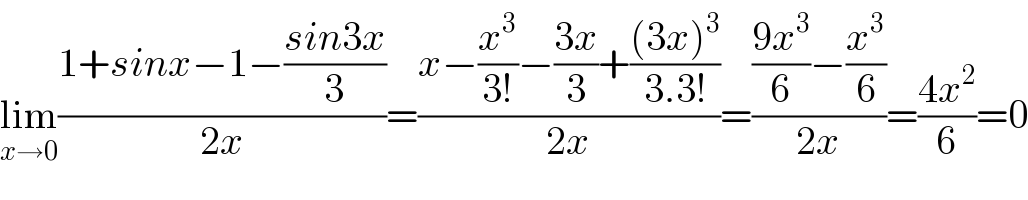
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}+{sinx}−\mathrm{1}−\frac{{sin}\mathrm{3}{x}}{\mathrm{3}}}{\mathrm{2}{x}}=\frac{{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}−\frac{\mathrm{3}{x}}{\mathrm{3}}+\frac{\left(\mathrm{3}{x}\right)^{\mathrm{3}} }{\mathrm{3}.\mathrm{3}!}}{\mathrm{2}{x}}=\frac{\frac{\mathrm{9}{x}^{\mathrm{3}} }{\mathrm{6}}−\frac{{x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{2}{x}}=\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{6}}=\mathrm{0} \\ $$
Commented by bemath last updated on 06/Aug/20

$$\mathrm{sin}\:\mathrm{x}\:=\:\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}!}+…? \\ $$
Commented by Dwaipayan Shikari last updated on 06/Aug/20
$${Oh}\:{i}\:{edited}\:{my}\:{error} \\ $$
Commented by bemath last updated on 06/Aug/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by john santu last updated on 06/Aug/20
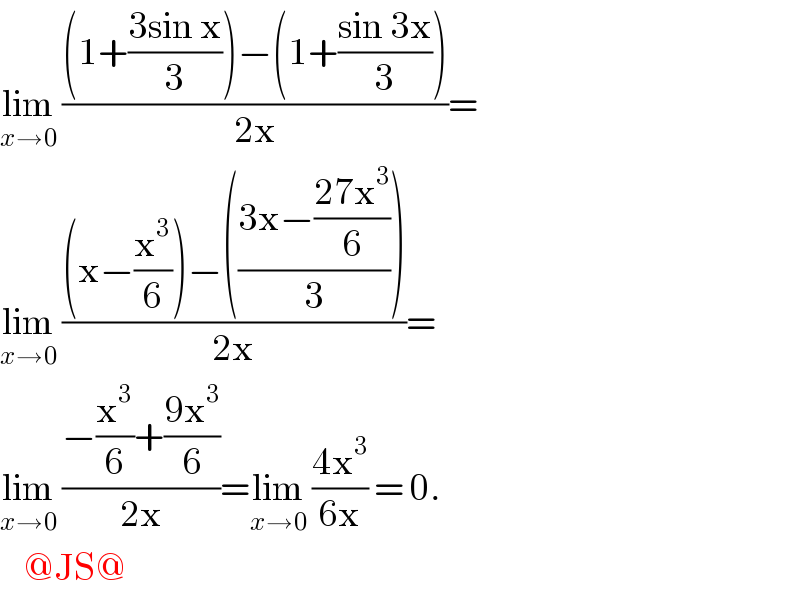
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}+\frac{\mathrm{3sin}\:\mathrm{x}}{\mathrm{3}}\right)−\left(\mathrm{1}+\frac{\mathrm{sin}\:\mathrm{3x}}{\mathrm{3}}\right)}{\mathrm{2x}}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)−\left(\frac{\mathrm{3x}−\frac{\mathrm{27x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{3}}\right)}{\mathrm{2x}}= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{\mathrm{9x}^{\mathrm{3}} }{\mathrm{6}}}{\mathrm{2x}}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{4x}^{\mathrm{3}} }{\mathrm{6x}}\:=\:\mathrm{0}. \\ $$$$\:\:\:\:@\mathrm{JS}@ \\ $$
Answered by 1549442205PVT last updated on 06/Aug/20
![Multiplying nominator and deminator by conjulate expression we get ((((1+3sin x ))^(1/3) −((1+sin 3x))^(1/3) )/(2x)) =(((1−3sinx)−(1+sin3x))/(x[(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) ==((3sinx−sin3x)/(x[(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) =(([3sinx−(3sinx−4sin^3 x])/(x[(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) =((sinx)/x)×((4sin^2 x)/(x[(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) Hence,lim_(x→0) ((((1+3sin x ))^(1/3) −((1+sin 3x))^(1/3) )/(2x))= lim_(x→0) =((sinx)/x)×((4sin^2 x)/([(^3 (√(1+3sinx)))^2 +^3 (√((1+3sinx)(1+sin3x)))+(^3 (√(1+sin3x)))^2 ])) =1×(0/(1+1+1))=0](https://www.tinkutara.com/question/Q106643.png)
$$\:\mathrm{Multiplying}\:\mathrm{nominator}\:\mathrm{and}\:\mathrm{deminator}\:\mathrm{by}\:\mathrm{conjulate}\:\mathrm{expression}\:\mathrm{we}\:\mathrm{get} \\ $$$$\:\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3sin}\:\mathrm{x}\:}\:−\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{3x}}}{\mathrm{2x}}\: \\ $$$$=\frac{\left(\mathrm{1}−\mathrm{3sinx}\right)−\left(\mathrm{1}+\mathrm{sin3x}\right)}{\mathrm{x}\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$==\frac{\mathrm{3sinx}−\mathrm{sin3x}}{\mathrm{x}\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$=\frac{\left[\mathrm{3sinx}−\left(\mathrm{3sinx}−\mathrm{4sin}^{\mathrm{3}} \mathrm{x}\right]\right.}{\mathrm{x}\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$=\frac{\mathrm{sinx}}{\mathrm{x}}×\frac{\mathrm{4sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$\mathrm{Hence},\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{3sin}\:\mathrm{x}\:}\:−\sqrt[{\mathrm{3}}]{\mathrm{1}+\mathrm{sin}\:\mathrm{3x}}}{\mathrm{2x}}= \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}=\frac{\mathrm{sinx}}{\mathrm{x}}×\frac{\mathrm{4sin}^{\mathrm{2}} \mathrm{x}}{\left[\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{3sinx}}\right)^{\mathrm{2}} +\:^{\mathrm{3}} \sqrt{\left(\mathrm{1}+\mathrm{3sinx}\right)\left(\mathrm{1}+\mathrm{sin3x}\right)}+\left(\:^{\mathrm{3}} \sqrt{\mathrm{1}+\mathrm{sin3x}}\right)^{\mathrm{2}} \right]} \\ $$$$=\mathrm{1}×\frac{\mathrm{0}}{\mathrm{1}+\mathrm{1}+\mathrm{1}}=\mathrm{0} \\ $$
